Question

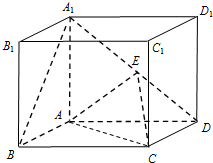如图，在长方体ABCD-A₁B₁C₁D₁中，A₁A=AD=

2

AB，E为线段A₁D上一点．
（Ⅰ）当E为A₁D的中点时，求证：直线A₁B∥平面EAC；
（Ⅱ）是否存在点E使二面角E-AC-D为30°？若存在，求

A1E

ED

，若不存在，说明理由．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（Ⅰ）设AC和BD交于点O，连EO，证明EO∥A₁B，利用仔细与平面平行的判定定理证明直线A₁B∥平面EAC．
（Ⅱ） 过E作EG⊥AD于G，过G作GH⊥AC于H，连EH，说明∠EHG为二面角E-AC-D的平面角，设EG=x，则DG=x，通过解三角形求出x，然后求出

A1E

ED

=3．

解答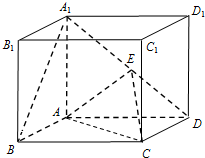： （Ⅰ）证明：设AC和BD交于点O，连EO，
由E，O分别是A₁D，BD的中点，故EO∥A₁B，…（4分）
∵EO?平面EAC，A₁B?平面EAC，
所以直线A₁B∥平面EAC．…（6分）
（Ⅱ）解：过E作EG⊥AD于G，过G作GH⊥AC于H，连EH，
∴EG⊥底面ABCD，∴EG⊥AC，
∴AC⊥面EGH，∴EH⊥AC，
∴∠EHG为二面角E-AC-D的平面角．…（10分）
设EG=x，则DG=x，
∴AG=2-x，又

HG

CD

=

AG

AC

，∴

HG

2

=

2-x

6

，∴HG=

2-x

3

，
∴tan∠EHG=

EG

GH

=

3 x

2-x

=

3

3

，∴x=

1

2

，
所以存在点E满足条件，且

A1E

ED

=3．…（15分）．

点评：本题考查二面角的平面角以及仔细与平面平行的判定，考查空间想象能力以及计算能力．