题目内容
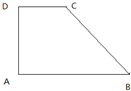在如图所示直角梯形ABCD中，AB∥DC，∠A=90°，AB=AD=2DC=4，画出该梯形的直观图A′B′C′D′，并写出其做法（要求保留作图过程的痕迹．）考点：斜二测法画直观图
专题：作图题,空间位置关系与距离
分析：根据平面图形的直观图的画法，即可得出结论．
解答：
解：（1）在已知的直角梯形ABCD中，以AB所在直线为x轴，垂直于AB的腰AD所在直线为y轴建立平面直角坐标系；
（2）画相应的x′轴和y′轴，使得∠x′O′y′=45°，在x′轴上取O′B′=AB，在y′轴上取O′D′=
AD，过D′作x′轴的平行线l，在l上沿x′轴正方向取点C′使得D′C′=DC；
（3）连接B′C′，所得四边形O′B′C′D′就是直角梯形ABCD的直观图．
解：（1）在已知的直角梯形ABCD中，以AB所在直线为x轴，垂直于AB的腰AD所在直线为y轴建立平面直角坐标系；（2）画相应的x′轴和y′轴，使得∠x′O′y′=45°，在x′轴上取O′B′=AB，在y′轴上取O′D′=
| 1 |
| 2 |
（3）连接B′C′，所得四边形O′B′C′D′就是直角梯形ABCD的直观图．
点评：本题考查平面图形的直观图的画法，及对斜二测画法的理解．属基础知识的考查．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
摩天轮中的数学问题．如图，游乐场中的摩天轮匀速旋转，其中心O距地面40.5m，半径40m，若从最低点处登上摩天轮，那么你与地面的距离将随着时间的变化，5min后达到最高点，你登上摩天轮的时刻开始计时．请求出你与地面的距离y与时间t的函数解析式．在△ABC中，BC=1，∠B=
，△ABC的面积S=
，则AC=（ ）
| π |
| 3 |
| 3 |
| A、4 | ||
B、
| ||
C、
| ||
D、
|
已知一个正方体的左视图和主视图都是长为2，宽为
的矩形，则该正方体的内切球的体积为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设a、b、c分别为△ABC三内角A、B、C的对边，若sinB≤2sinCcosA，c=2bcosA，则sin（2A+
）的取值范围是（ ）
| π |
| 3 |
| A、（0，1] | ||
| B、[0，1] | ||
C、（
| ||
D、[0，
|
函数f（x）=
sin（ωx+φ）（x∈R，ω＞0，|φ|＜
）的部分图象如图所示，则ω的值是（ ）
| 2 |
| π |
| 2 |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|