题目内容
15．从集合A={1，2，3，4，5，6，7，8，9，10}中任取两个数，欲使取到的一个数大于k，另一个数小于k（其中k∈A）的概率为$\frac{2}{5}$，则k=4或7．分析 由题意$\frac{（10-k）（k-1）}{{C}_{10}^{2}}$=$\frac{2}{5}$，由此能求出结果．
解答 解：∵从集合A={1，2，3，4，5，6，7，8，9，10}中任取两个数，
欲使取到的一个数大于k，另一个数小于k（其中k∈A）的概率为$\frac{2}{5}$，
∴$\frac{（10-k）（k-1）}{{C}_{10}^{2}}$=$\frac{2}{5}$，
解得k=4或k=7．
故答案为：4或7．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
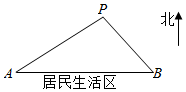如图所示，A，B是两个垃圾中转站，B在A的正东方向16千米处，AB的南面为居民生活区，为了妥善处理生活垃圾，政府决定在AB的背面建一个垃圾发电厂P，垃圾发电厂P的选址拟满足以下两个要求（A，B，P可看成三个点）：
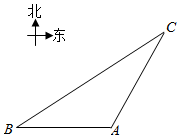如图，一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾，红外线感应测量发现机器人到B的距离比到C的距离少0.4m，于是选择沿A→B→C路线清扫，已知智能扫地机器人的直线行走速度为0.2m/s，忽略机器人吸入垃圾及在B处旋转所用时间，10秒钟完成了清扫任务；
10．记集合A={x|x-a＞0}，B={y|y=sinx，x∈R}，若0∈A∩B，则a的取值范围是（ ）
| A． | （-∞，0） | B． | （-∞，0] | C． | [0，+∞） | D． | （0，+∞） |
20．盒中共有6件除了颜色外完全相同的产品，其中有1件红色，2件白色和3件黑色，从中任取两件，则两件颜色不相同的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{7}{15}$ | C． | $\frac{3}{5}$ | D． | $\frac{11}{15}$ |
7．“$θ=2kπ+\frac{π}{4}（k∈Z）$”是“tanθ=1”的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分也不必要条件 |