题目内容
3.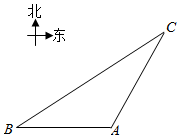 如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;
如图,一智能扫地机器人在A处发现位于它正西方向的B处和B处和北偏东30°方向上的C处分别有需要清扫的垃圾,红外线感应测量发现机器人到B的距离比到C的距离少0.4m,于是选择沿A→B→C路线清扫,已知智能扫地机器人的直线行走速度为0.2m/s,忽略机器人吸入垃圾及在B处旋转所用时间,10秒钟完成了清扫任务;(1)求B、C两处垃圾之间的距离;(精确到0.1)
(2)求智能扫地机器人此次清扫行走路线的夹角∠B的大小;(用反三角函数表示)
分析 (1)设BC=x,则AB=2-x,AC=2.4-x,A=120°,利用余弦定理列方程解出x;
(2)利用(1)的结论得出三角形ABC的三边长,使用余弦定理求出cosB,得到B的大小.
解答 解;(1)设BC=x,则AB=2-x,AC=2-x+0.4=2.4-x,
由题意得A=120°,
在△ABC中,由余弦定理得:cosA=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB×AC}$=$\frac{(2-x)^{2}+(2.4-x)^{2}-{x}^{2}}{2×(2-x)×(2.4-x)}$=-$\frac{1}{2}$.
解得x=1.4.
∴BC=1.4m.
(2)由(1)知AB=0.6,AC=1,BC=1.4.
∴cosB=$\frac{A{B}^{2}+B{C}^{2}-A{C}^{2}}{2AB•BC}$=$\frac{11}{14}$.
∴B=arccos$\frac{11}{14}$.
点评 本题考查了余弦定理,解三角形的实际应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.下列命题:
①“若a≤b,则a<b”的否命题;
②“若a=1,则ax2-x+3≥0的解集为R”的逆否命题;
③“周长相同的圆面积相等”的逆命题;
④“若$\sqrt{2}x$为有理数,则x为无理数”的逆否命题.
其中真命题序号为( )
①“若a≤b,则a<b”的否命题;
②“若a=1,则ax2-x+3≥0的解集为R”的逆否命题;
③“周长相同的圆面积相等”的逆命题;
④“若$\sqrt{2}x$为有理数,则x为无理数”的逆否命题.
其中真命题序号为( )
| A. | ②④ | B. | ①②③ | C. | ②③④ | D. | ①②③④ |
14.已知直线l与平面α相交但不垂直,m为空间内一条直线,则下列结论可能成立的是( )
| A. | m∥l,m⊥α | B. | m∥l,m∥α | C. | m⊥l,m⊥α | D. | m⊥l,m∥α |
8.据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改”引起广泛关注.为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3000人进行调查,就“是否取消英语听力”的问题进行了问卷调查统计,结果如表:
已知在全体样本中随机抽取1人,抽到持“应该保留”态度的人的概率为0.06.
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
| 态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
| 在校学生 | 2100人 | 120人 | y人 |
| 社会人士 | 500人 | x人 | z人 |
(Ⅰ)现用分层抽样的方法在所有参与调查的人中抽取300人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(Ⅱ)在持“应该保留”态度的人中,用分层抽样的方法抽取6人,然后从这6人中随机抽取2人,求这2人中恰好有1个人为在校学生的概率.
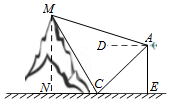 如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m.
如图,无人机在离地面高200m的A处,观测到山顶M处的仰角为15°、山脚C处的俯角为45°,已知∠MCN=60°,则山的高度MN为300m. 函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则ω=2,φ=$\frac{π}{6}$.
函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则ω=2,φ=$\frac{π}{6}$.