题目内容
1.已知(x,y)满足$\left\{\begin{array}{l}y≥x\\ y≤2\\ y≥2-x\end{array}$,z=x+ay,若z取得最大值的最优解有无数个,则a=( )| A. | 1 | B. | -1 | C. | 1或-1 | D. | 无法确定 |
分析 由题设条件,目标函数z=x+ay,取得最大值的最优解有无数个知取得最优解必在边界上而不是在顶点上,目标函数x+ay=0应与直线BC平行;进而计算可得答案.
解答  解:由题意,$\left\{\begin{array}{l}y≥x\\ y≤2\\ y≥2-x\end{array}$的可行域如图:
解:由题意,$\left\{\begin{array}{l}y≥x\\ y≤2\\ y≥2-x\end{array}$的可行域如图:
z=x+ay,若z取得最大值的最优解有无数个,
最优解应在线段BC上取得,故x+ay=0应与直线BC平行
∵kBC=1,
∴a=-1,
故选:B.
点评 本题考查线性规划最优解的判定,属于该知识的逆用题型,知最优解的特征,判断出最优解的位置求参数.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
11.已知tanα=$\sqrt{3},π<α<\frac{3π}{2}$,则$cos2α-sin({\frac{π}{2}+α})$=( )
| A. | 0 | B. | -1 | C. | 1 | D. | $\frac{{\sqrt{3}-1}}{2}$ |
9.已知条件p:|x-4|≤6,条件q:x≤1+m,若p是q的充分不必要条件,则m的取值范围是( )
| A. | (-∞,-1] | B. | (-∞,9] | C. | [1,9] | D. | [9,+∞) |
16.过球O表面上一点A引三条长度相等的弦AB、AC、AD,且两两夹角都为60°,若球半径为R,则弦AB的长度为( )
| A. | $\frac{{2\sqrt{6}}}{3}R$ | B. | $\frac{{\sqrt{6}}}{3}R$ | C. | R | D. | $\sqrt{6}R$ |
10.已知向量$\overrightarrow a=({1,2}),\overrightarrow b=({-2,m})$,若$\overrightarrow a∥\overrightarrow b$,则m=( )
| A. | -1 | B. | -4 | C. | 4 | D. | 1 |
11.钱大妈常说“便宜没好货”,她这句话的意思中:“好货”是“不便宜”的( )
| A. | 充分条件 | B. | 必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
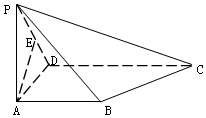 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ADC=90°,$AD=AB=\frac{1}{2}CD=1$,PA⊥平面ABCD,E为PD中点,且PC⊥AE.