题目内容

20．过点（1，1）的抛物线y=ax2的焦点坐标为（　　）
A．$（{-\frac{1}{4}，0}）$B．$（{0，-\frac{1}{4}}）$C．$（{0，\frac{1}{4}}）$D．$（{\frac{1}{4}，0}）$

分析 利用抛物线经过的点，推出a，然后化简抛物线方程为标准方程，求解焦点坐标即可．

解答 解：点（1，1）在抛物线y=ax2的图象上，可得a=1．
抛物线y=x2的焦点坐标为：（0，$\frac{1}{4}$）．
故选：C．

点评 本题考查抛物线的简单性质的应用，考查计算能力．

练习册系列答案
相关题目
4．已知函数f（x）=2lnx-3x2-11x．
（1）求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）若关于x的不等式f（x）≤（a-3）x2+（2a-13）x-2恒成，求整数a的最小值；
（3）若正实数x1，x2满足f（x1）+f（x2）+4（x12+x22）+12（x1+x2）=4，证明：x1+x2≥2．
11．已知tanα=$\sqrt{3}，π＜α＜\frac{3π}{2}$，则$cos2α-sin（{\frac{π}{2}+α}）$=（　　）
A．0B．-1C．1D．$\frac{{\sqrt{3}-1}}{2}$
8．已知实数x，y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$，则目标函数z=2y-x的最大值为（　　）
A．14B．13C．12D．11
15．甲、乙两校各有3名教师报名支教，其中甲校2男1女，乙校1男2女．
（Ⅰ）若从甲校和乙校报名的教师中各任选1名，求选出的2名教师性别相同的概率；
（Ⅱ）若从报名的6名教师中任选2名，求选出的2名教师来自同一学校的概率．
5．已知过抛物线y2=8x的焦点F的直线与抛物线交于A，B两点，且|AB|=10，则|AF|•|BF|=20．
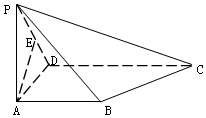12．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，∠ADC=90°，$AD=AB=\frac{1}{2}CD=1$，PA⊥平面ABCD，E为PD中点，且PC⊥AE．
（1）求证：PA=AD；
（2）求点A到平面PBC的距离．
9．已知条件p：|x-4|≤6，条件q：x≤1+m，若p是q的充分不必要条件，则m的取值范围是（　　）
A．（-∞，-1]B．（-∞，9]C．[1，9]D．[9，+∞）
10．已知向量$\overrightarrow a=（{1，2}），\overrightarrow b=（{-2，m}）$，若$\overrightarrow a∥\overrightarrow b$，则m=（　　）
A．-1B．-4C．4D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网