题目内容
已知-
<x<0,sinx+cosx=
.
(1)求sinx•cosx的值;
(2)求sinx-cosx的值;
(3)求
的值.
| π |
| 2 |
| 1 |
| 5 |
(1)求sinx•cosx的值;
(2)求sinx-cosx的值;
(3)求
| 2sinxcosx+2sin2x |
| 1-tanx |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:首先对已知条件和恒等关系式sin2θ+cos2θ=1、tanθ=
进行恒等变换,然后构建成方程组求得相关的结果.
| sinθ |
| cosθ |
解答:
解:(1)将sinx+cosx=
两边平方得:(sinx+cosx)2=1+2sinxcosx=
,
则sinxcosx=-
(2)∵sinxcosx=-
,-
<x<0,
∴sinx-cosx=-|sinx-cosx|=-
=-
(3)由(1),(2)可知
解得:
=
=-
故答案为:(1)sinxcosx=-
(2)sinx-cosx=-
(3)
=-
| 1 |
| 5 |
| 1 |
| 25 |
则sinxcosx=-
| 12 |
| 25 |
(2)∵sinxcosx=-
| 12 |
| 25 |
| π |
| 2 |
∴sinx-cosx=-|sinx-cosx|=-
| 1-2sinxcosx |
| 7 |
| 5 |
(3)由(1),(2)可知
|
解得:
|
| 2sinxcosx+2sin2x |
| 1-tanx |
| 2sinxcosx+2sin2x | ||
1-
|
| 24 |
| 175 |
故答案为:(1)sinxcosx=-
| 12 |
| 25 |
(2)sinx-cosx=-
| 7 |
| 5 |
(3)
| 2sinxcosx+2sin2x |
| 1-tanx |
| 24 |
| 175 |
点评:本题考查的知识点:同角三角函数的恒等变换,sin2θ+cos2θ=1、tanθ=
及相关的运算问题.
| sinθ |
| cosθ |

练习册系列答案
相关题目
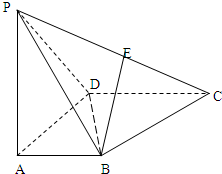 四棱锥P-ABCD中,ABCD为平行四边形,PA⊥底面ABCD,∠BAC=30°,PA=BD,
四棱锥P-ABCD中,ABCD为平行四边形,PA⊥底面ABCD,∠BAC=30°,PA=BD,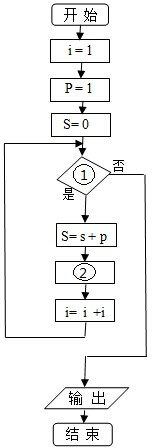 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将下面给出的程序框图补充完整,再根据程序框图写出程序.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将下面给出的程序框图补充完整,再根据程序框图写出程序.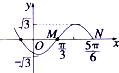 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,若函数g(x)与函数f(x)的图象关于点P(
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示,若函数g(x)与函数f(x)的图象关于点P(