题目内容
4.将函数y=2sin(x+$\frac{π}{3}$)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,再将所得图象向右平移$\frac{π}{4}$个单位长度,得到函数f(x)的图象,则( )| A. | f(x)在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递减 | B. | f(x)在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上单调递增 | ||
| C. | f(x)的图象关于直线x=-$\frac{5π}{12}$对称 | D. | f(x)的图象关于点($\frac{7π}{12}$,0)对称. |
分析 根据三角函数的图象变换关系,求出函数f(x)的解析式,然后根据三角函数的性质分别进行判断即可.
解答 解:将函数y=2sin(x+$\frac{π}{3}$)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,得到数y=2sin(2x+$\frac{π}{3}$),
再将所得图象向右平移$\frac{π}{4}$个单位长度,得到数y=2sin[2(x-$\frac{π}{4}$)+$\frac{π}{3}$]=2sin(2x-$\frac{π}{6}$),
即f(x)=2sin(2x-$\frac{π}{6}$),
当-$\frac{π}{3}$≤x≤$\frac{π}{6}$,则-$\frac{2π}{3}$≤2x≤$\frac{π}{3}$,则-$\frac{5π}{6}$≤2x-$\frac{π}{6}$≤$\frac{π}{6}$,则函数f(x)不是单调函数,即函数f(x)在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上不是单调函数,故A,B错误.
f(-$\frac{5π}{12}$)=2sin[2×(-$\frac{5π}{12}$)-$\frac{π}{6}$]=2sin(-π)=0,则函数关于(-$\frac{5π}{12}$,0)对称,故C错误,
f($\frac{7π}{12}$)=2sin(2×$\frac{7π}{12}$-$\frac{π}{6}$)=2sinπ=0,则函数关于($\frac{7π}{12}$,0)对称,故D正确,
故选:D.
点评 本题主要考查命题的真假判断,涉及三角函数的解析式,三角函数的单调性和对称性的性质,求出函数的解析式是解决本题的关键.

练习册系列答案
相关题目
14.已知z为纯虚数,且(2+i)z=1+ai3(i为虚数单位),则|a+z|=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
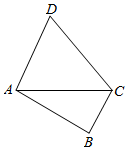 如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.
如图所示,在四边形ABCD中,已知AC=$\sqrt{6}+\sqrt{2}$,AD=2$\sqrt{2}$,DC=2$\sqrt{3}$,AD∥BC.