题目内容
19．命题“?x∈R，x3-x≥0”的否定是（ ）| A． | ?x∈R，x3-x＜0 | B． | ?x∈R，x3-x≥0 | C． | ?x∈R，x3-x＞0 | D． | ?x∈R，x3-x＜0 |
分析 根据全称命题的否定是特称命题进行判断即可．
解答 解：命题是全称命题，
则命题的否定是?x∈R，x3-x＜0，
故选：D．
点评 本题主要考查含有量词的命题的否定，比较基础．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
10．已知角α的终边上一点P的坐标为（sin$\frac{2π}{3}$，cos$\frac{2π}{3}$），则角α的最小正角为（ ）
| A． | $\frac{5π}{3}$ | B． | $\frac{2}{3}$π | C． | $\frac{5}{6}$π | D． | $\frac{11}{6}$π |
7．执行如图所示的程序框图，若输入n的值为3，则输出S的值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
8．
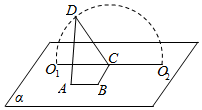如图，A，B，C，O1，O2∈平面α，AB=BC=$\sqrt{3}$，∠ABC=90°，D为动点，DC=2，且DC丄BC，当点D从O1，顺时针转动到O2的过程中（D与O1、O2不重合），异面直线AD与BC所成角（ ）
如图，A，B，C，O1，O2∈平面α，AB=BC=$\sqrt{3}$，∠ABC=90°，D为动点，DC=2，且DC丄BC，当点D从O1，顺时针转动到O2的过程中（D与O1、O2不重合），异面直线AD与BC所成角（ ）| A． | 一直变小 | B． | 一直变大 | ||
| C． | 先变小，后变大 | D． | 先变小，再变大，后变小 |