题目内容
8.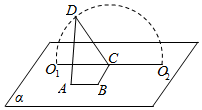 如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )
如图,A,B,C,O1,O2∈平面α,AB=BC=$\sqrt{3}$,∠ABC=90°,D为动点,DC=2,且DC丄BC,当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),异面直线AD与BC所成角( )| A. | 一直变小 | B. | 一直变大 | ||
| C. | 先变小,后变大 | D. | 先变小,再变大,后变小 |
分析 以C为原点,CB为x轴,CO2为y轴,过C作平面ABC的垂线为z轴,建立空间直角坐标系,利用向量法能求出结果.
解答 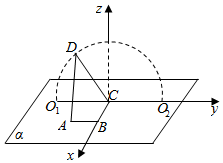 解:以C为原点,CB为x轴,CO2为y轴,过C作平面ABC的垂线为z轴,建立空间直角坐标系,
解:以C为原点,CB为x轴,CO2为y轴,过C作平面ABC的垂线为z轴,建立空间直角坐标系,
B($\sqrt{3}$,0,0),C(0,0,0),A($\sqrt{3}$,-$\sqrt{3}$,0),设O1O2=2t,∠O2CD=θ,0°≤θ≤180°,
则CD=t,D(0,tcosθ,tsinθ),
$\overrightarrow{CB}$=($\sqrt{3}$,0,0),$\overrightarrow{AD}$=(-$\sqrt{3}$,tcosθ+$\sqrt{3}$,tsinθ),
设异面直线AD与BC所成角为α,
则cosα=$\frac{|\overrightarrow{AD},\overrightarrow{CB}|}{|\overrightarrow{AD}|•|\overrightarrow{CB}|}$=$\frac{3}{\sqrt{3}•\sqrt{3+(tcosθ+\sqrt{3})^{2}+(tsinθ)^{2}}}$=$\frac{\sqrt{3}}{\sqrt{6+{t}^{2}+2\sqrt{3}tcosθ}}$,
∵当点D从O1,顺时针转动到O2的过程中(D与O1、O2不重合),
cosθ从-1增加到1,cosα在(0,1)内递减,
∴异面直线AD与BC所成角一直变小.
故选:A.
点评 本题考查异面直线所成角的变化范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
19.命题“?x∈R,x3-x≥0”的否定是( )
| A. | ?x∈R,x3-x<0 | B. | ?x∈R,x3-x≥0 | C. | ?x∈R,x3-x>0 | D. | ?x∈R,x3-x<0 |
20.某产品的广告费用x与销售额y的统计数据如表
已知由表中4组数据求得回归直线方程$\stackrel{∧}{y}$=8x+14,则表中的a的值为( )
| 广 告 费 用x (万元) | 4 | 2 | 3 | 5 |
| 销 售 额y (万元) | 49 | 26 | a | 54 |
| A. | 37 | B. | 38 | C. | 39 | D. | 40 |
17.已知顶点在原点,关于y轴对称的抛物线与直线x-2y=1交于P,Q两点,若|PQ|=$\sqrt{15}$,则抛物线的方程为( )
| A. | x2=-4y | B. | x2=12y | C. | x2=-4y或x2=12y | D. | 以上都不是 |