已知复数z=$\frac{2-{i}^{2017}}{1+i}$.则z的共轭复数在复平面内对应的点位于( )A．第一象限B．第二象限C．第三象限D．第四象限题目和参考答案——青夏教育精英家教网—

题目内容

19．已知复数z=$\frac{2-{i}^{2017}}{1+i}$，则z的共轭复数在复平面内对应的点位于（　　）

A．

第一象限

B．

第二象限

C．

第三象限

D．

第四象限

分析利用虚数单位i得性质及复数代数形式的乘除运算化简求得z，进一步求出$\overline{z}$得答案．

解答解：∵z=$\frac{2-{i}^{2017}}{1+i}$=$\frac{2-（{i}^{4}）^{504}•i}{1+i}=\frac{2-i}{1+i}=\frac{（2-i）（1-i）}{（1+i）（1-i）}$=$\frac{1-3i}{2}$=$\frac{1}{2}-\frac{3}{2}i$，
∴$\overline{z}=\frac{1}{2}+\frac{3}{2}i$，
∴z的共轭复数在复平面内对应的点的坐标为（$\frac{1}{2}，\frac{3}{2}$），位于第一象限．
故选：A．

点评本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

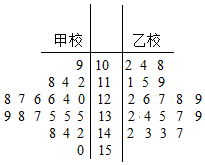
9．

一次数学考试后，某老师从自己所带的两个班级中各抽取6人，记录他们的考试成绩，得到如图所示的茎叶图．已知甲班6名同学成绩的平均数为82，乙班6名同学成绩的中位数为77，则x-y=（　　）

10．

某市在对高三学生的4月理科数学调研测试的数据统计显示，全市10000名学生的成绩服从正态分布X～N（110，144），现从甲校100分以上的200份试卷中用系统抽样的方法抽取了20份试卷来分析，统计如下：

试卷编号	n₁	n₂	n₃	n₄	n₅	n₆	n₇	n₈	n₉	n₁₀
试卷得分	109	118	112	114	126	128	127	124	126	120
试卷编号	n₁₁	n₁₂	n₁₃	n₁₄	n₁₅	n₁₆	n₁₇	n₁₈	n₁₉	n₂₀
试卷得分	135	138	135	137	135	139	142	144	148	150

（注：表中试卷编号n₁＜n₂＜28＜n₄＜n₅＜…＜n₂₀）

（1）列出表中试卷得分为126分的试卷编号（写出具体数据）；
（2）该市又从乙校中也用系统抽样的方法抽取了20份试卷，将甲乙两校这40份试卷的得分制作了茎叶图（如图），试通过茎叶图比较两校学生成绩的平均分及分散程度（均不要求计算出具体值，给出结论即可）；
（3）在第（2）问的前提下，从甲乙两校这40名学生中，从成绩在140分以上（含140分）的学生中任意抽取3人，该3人在全市前15名的人数记为ξ，求ξ的分布列和期望．
（附：若随机变量X服从正态分布N（μ，σ²），则P（μ-σ＜X＜μ+σ）=68.3%，P（μ-2σ＜X＜μ+2σ）=95.4%，P（μ-3σ＜X＜μ+3σ）=99.7%）

7．下列判断正确的是（　　）

	A．	若事件A与事件B互斥，则事件A与事件B对立
	B．	函数y=$\sqrt{{x}^{2}+9}+\frac{1}{\sqrt{{x}^{2}+9}}$（x∈R）的最小值为2
	C．	若直线（m+1）x+my-2=0与直线mx-2y+5=0互相垂直，则m=1
	D．	“p∧q为真命题”是“p∨q为真命题”的充分不必要条件

14．定义在R上的偶函数f（x）满足f（1-x）=f（1+x），且当x∈[0，1]时，f（x）=$\sqrt{2x-{x}^{2}}$．则直线x-4y+2=0与曲线y=f（x）的交点个数为（　　）

4．已知集合M={x|x＞2}，N={x|1＜x＜3}，则N∩∁_RM=（　　）