��Ŀ����
20����֪����Ϊ��ĺ���f��x���ڶ�����[0��1]�ϵ�ͼ����������ϣ���������f��0��=f��1��=0���Ҷ�����x1��x2��[0��1]����|f��x1��-f��x2��|��$\frac{1}{3}$|x1-x2|����������ĸ����ۣ�����f��1-x��=f��x����0��x��$\frac{1}{2}$ʱ��f��x��=$\frac{1}{20}$x��x-$\frac{1}{2}$������$\frac{1}{2}$��x��1ʱ��f��x��=$\frac{1}{20}$��1-x����$\frac{1}{2}$-x����
������?x��[0��1]����f��1-x��=-f��x������y=f��x��������3����㣻
�۶�?x��[0��1]��|f��x��|��$\frac{1}{6}$�������
�ܶ�?x1��x2��[0��1]��|f��x1��-f��x2��|��$\frac{1}{6}$�������
������ȷ�Ľ��۸����У�������
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� ������֪��f��0��=f��1��=0���Ҷ�����x1��x2��[0��1]����|f��x1��-f��x2��|��$\frac{1}{3}$|x1-x2|����һ�����ĸ����۵���٣��ɵô𰸣�
��� �⣺��f��1-x��=f��x���ú���f��x��ͼ�����ֱ��x=$\frac{1}{2}$�Գƣ�
��0��x��$\frac{1}{2}$ʱ��f��x��=$\frac{1}{20}$x��x-$\frac{1}{2}$������$\frac{1}{2}$��x��1ʱ��f��x��=$\frac{1}{20}$��1-x����$\frac{1}{2}$-x�����ʢ���ȷ��
��f��1-x��=-f��x�����ʺ���ͼ����ڣ�$\frac{1}{2}$��0���Գƣ�
����f��0��=f��1��=0��
�ʺ���f��x��������3�����0��$\frac{1}{2}$��1���ʢ���ȷ��
�ߵ�0��x��$\frac{1}{2}$ʱ��|f��x��|��$\frac{1}{3}$x��$\frac{1}{6}$��
��$\frac{1}{2}$��x��1ʱ����1-x��$\frac{1}{2}$��
|f��x��|=|f��x��-f��1��|��$\frac{1}{3}$��1-x����$\frac{1}{3}��\frac{1}{2}$=$\frac{1}{6}$��
��?x��[0��1]��|f��x��|��$\frac{1}{6}$��������ʢ���ȷ��
��?x1��x2��[0��1]����|x1-x2|��$\frac{1}{2}$ʱ��|f��x1��-f��x2��|��$\frac{1}{3}$|x1-x2|��$\frac{1}{6}$��
��|x1-x2|��$\frac{1}{2}$ʱ��|f��x1��-f��x2��|=|f��x1��-f��0��+f��1��-f��x2��|
��|f��x1��-f��0��|+|f��1��-f��x2��|��$\frac{1}{3}$|x1-0|+$\frac{1}{3}$|1-x2|
=$\frac{1}{3}$��1+$\frac{1}{3}$��1-x2��=$\frac{1}{3}$-$\frac{1}{3}$��x2-x1����$\frac{1}{3}$-$\frac{1}{3}$��$\frac{1}{2}$=$\frac{1}{6}$���ʢ���ȷ
��ѡD��
���� ���������������ж���Ӧ��Ϊ���壬�����˺����ĶԳ��ԣ��������������������㣬����ֵ���Dz���ʽ��֪ʶ�㣬�Ѷ��е���

 ��У����ϵ�д�
��У����ϵ�д�| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 1+$\sqrt{2}$ | D�� | 1+$\sqrt{3}$ |
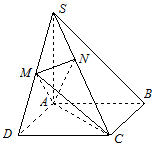 ��ͼ��������S-ABCD�У�����ABCD�������Σ�SA�͵���ABCD��SA=AB=2����M��SD���е㣬AN��SC���ҽ�SC�ڵ�N��
��ͼ��������S-ABCD�У�����ABCD�������Σ�SA�͵���ABCD��SA=AB=2����M��SD���е㣬AN��SC���ҽ�SC�ڵ�N��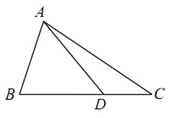 ��ͼ���ڡ�ABC�У�AB=2��cosB=$\frac{1}{3}$����D���߶�BC�ϣ�
��ͼ���ڡ�ABC�У�AB=2��cosB=$\frac{1}{3}$����D���߶�BC�ϣ�