题目内容
1．
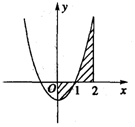由曲线y=x 2-1，直线x=0，x=2和x轴围成的封闭图形的面积（如图）可表示为（ ）| A． | ${∫}_{0}^{2}$（x 2-1）dx | B． | ${∫}_{0}^{2}$|（x 2-1）|dx | ||
| C． | |${∫}_{0}^{2}$（x 2-1）dx| | D． | ${∫}_{0}^{1}$（x 2-1）dx+${∫}_{1}^{2}$（x 2-1）dx |
分析 利用定积分的几何意义利用得分表示封闭图形的面积即可．
解答 解：由曲线y=x 2-1，直线x=0，x=2和x轴围成的封闭图形的面积
${∫}_{0}^{1}$（1-x 2）dx+${∫}_{1}^{2}$（x 2-1）dx=${∫}_{0}^{2}$|（x 2-1）|dx；
故选B．
点评 本题考查了定积分的运用；正确利用定积分与封闭图形面积的关系是关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．在平面直角坐标系xOy中，以C（1，1）为圆心的圆与x轴和y轴分别相切于A，B两点，点M，N分别在线段OA，OB上，若，MN与圆C相切，则|MN|的最小值为（ ）
| A． | 1 | B． | $2-\sqrt{2}$ | C． | $2\sqrt{2}+2$ | D． | $2\sqrt{2}-2$ |
6．给出定义：如果函数f（x）在区间[a，b]上可导，其导函数为f'（x），且?x1，x2∈（a，b），当x1≠x2时总满足：f'（x1）=$\frac{f（b）-f（a）}{b-a}$，f'（x2）=$\frac{f（a）-f（b）}{a-b}$，则称实数x1，x2为[a，b]上的“希望数”，函数f（x）为[a，b]上的“希望函数”．如果函数f（x）=$\frac{1}{3}$x3-x2+k是[0，k]上的“希望函数”，那么实数k的取值范围是（ ）
| A． | （$\frac{3}{2}$，3） | B． | （2，3） | C． | （$\frac{3}{2}$，2$\sqrt{3}$） | D． | （2，2$\sqrt{3}$） |
11．函数sgn（x）=$\left\{\begin{array}{l}{-1，x＜0}\\{0，x=0}\\{1，x＞0}\end{array}\right.$叫做符号函数，则不等式x+（x+2）sgn（x+1）≤4的解集为（ ）
| A． | （-∞，1] | B． | （-1，1） | C． | （-1，1] | D． | [-1，1] |