题目内容
10.已知函数f(x)=2$\sqrt{3}$sinxcosx-cos2x(Ⅰ)求f(x)的最小正周期;
(Ⅱ)求函数f(x)在区间[0,$\frac{2π}{3}$]上的取值范围.
分析 (Ⅰ)先利二倍角和辅助角公式将函数化为y=Asin(ωx+φ)的形式,再利用周期公式求函数的最小正周期.
(Ⅱ)x∈[0,$\frac{2π}{3}$]上时,求出内层函数的取值范围,结合三角函数的图象和性质,求出f(x)的取值最大和最小值,即得到f(x)的取值范围.
解答 解:(Ⅰ)函数f(x)=2$\sqrt{3}$sinxcosx-cos2x,
化简可得:f(x)=$\sqrt{3}$sin2x-cos2x=2sin(2x-$\frac{π}{6}$)
函数的最小正周期T=$\frac{2π}{ω}=\frac{2π}{2}=π$.
(Ⅱ)x∈[0,$\frac{2π}{3}$]上时,
2x-$\frac{π}{6}$∈[$-\frac{π}{6}$,$\frac{7π}{6}$]
当2x-$\frac{π}{6}$=$-\frac{π}{6}$或$\frac{7π}{6}$时,函数f(x)的取值最小值为-1,
当2x-$\frac{π}{6}$=$\frac{π}{2}$时,函数f(x)的取值最大值为2,
故得函数f(x)在区间[0,$\frac{2π}{3}$]上的取值范围是[-1,2].
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于基础题.

练习册系列答案
相关题目
20.若函数f(x)=$\left\{\begin{array}{l}\frac{a}{x},x>1\\(2-3a)x+1,x≤1\end{array}$是R上的减函数,则实数R的取值范围是 ( )
| A. | $(\frac{2}{3},1)$ | B. | $[\frac{3}{4},1)$ | C. | $(\frac{2}{3},\frac{3}{4}]$ | D. | ($\frac{2}{3}$,+∞) |
1.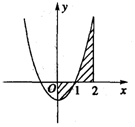 由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
 由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )
由曲线y=x 2-1,直线x=0,x=2和x轴围成的封闭图形的面积(如图)可表示为( )| A. | ${∫}_{0}^{2}$(x 2-1)dx | B. | ${∫}_{0}^{2}$|(x 2-1)|dx | ||
| C. | |${∫}_{0}^{2}$(x 2-1)dx| | D. | ${∫}_{0}^{1}$(x 2-1)dx+${∫}_{1}^{2}$(x 2-1)dx |
18.在△ABC中,A=$\frac{π}{6},BC=\frac{{4\sqrt{3}}}{3}$,AB=4,则C=( )
| A. | $\frac{π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$或$\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
5.f(x)是定义在R上图形关于y轴对称,且在[0,+∞)上是减函数,下列不等式一定成立的是( )
| A. | f[${\frac{2}{{2-{a^2}}}}$]<f(${{a^2}-2a+\frac{5}{4}}$) | B. | f[-cos60°]<f(tan30°) | ||
| C. | f[-(cos60°)2]≥f(${{a^2}-2a+\frac{5}{4}}$) | D. | f[-sin45°]>f(-3a+2) |
20.在△ABC中,角A,B,C所对的边分别为a,b,c,且满足b2+c2-a2=bc,$\overrightarrow{AB}$•$\overrightarrow{BC}$>0,a=$\frac{\sqrt{3}}{2}$,则b+c的取值范围是( )
| A. | (1,$\frac{3}{2}$) | B. | ($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$) | C. | ($\frac{1}{2}$,$\frac{3}{2}$) | D. | ($\frac{1}{2}$,$\frac{3}{2}$] |