题目内容
6.已知函数$f(x)=2sin(ωx+ϕ)+1,(ω>0,|ϕ|≤\frac{π}{2})$,其图象与直线y=-1相邻两个交点的距离为π,若f(x)>1对任意$x∈(-\frac{π}{12},\frac{π}{3})$恒成立,则ϕ的取值范围是( $\frac{π}{6}$,$\frac{π}{3}$).分析 由题意可得当x∈(-$\frac{π}{12}$,$\frac{π}{3}$)时,sin(2x+ϕ)>0,再利用正弦函数的图象和性质,求得ϕ的取值范围.
解答 解:∵函数$f(x)=2sin(ωx+ϕ)+1,(ω>0,|ϕ|≤\frac{π}{2})$,令f(x)=-1,可得sin(ωx+ϕ)=-1,
由于f(x)的图象与直线y=-1相邻两个交点的距离为π,∴T=$\frac{2π}{ω}$=π,∴ω=2,f(x)=2sin(2x+ϕ)+1.
若f(x)>1对任意$x∈(-\frac{π}{12},\frac{π}{3})$恒成立,则当x∈(-$\frac{π}{12}$,$\frac{π}{3}$)时,sin(2x+ϕ)>0,
∴2•(-$\frac{π}{12}$)+ϕ>2kπ,且2•$\frac{π}{3}$+ϕ<2kπ+π,k∈Z,即2kπ+$\frac{π}{3}$>ϕ>2kπ+$\frac{π}{6}$,∴ϕ∈( $\frac{π}{6}$,$\frac{π}{3}$).
故答案为:( $\frac{π}{6}$,$\frac{π}{3}$).
点评 本题主要考查正弦函数的图象和性质,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
1.已知函数f(x)=sinx-λcosx的图象的一个对称中心是($\frac{π}{3}$,0),则函数g(x)=λsinxcosx+sin2x图象的一条对称轴是( )
| A. | x=-$\frac{π}{3}$ | B. | x=$\frac{2π}{3}$ | C. | x=$\frac{π}{6}$ | D. | x=$\frac{5π}{6}$ |
11.若数列{an},{bn}的通项公式分别为an=(-1)n+2016•a,bn=2+$\frac{{{{(-1)}^{n+2017}}}}{n}$,且an<bn,对任意n∈N*恒成立,则实数a的取值范围是( )
| A. | $[-1,\frac{1}{2})$ | B. | [-1,1) | C. | [-2,1) | D. | $[-2,\frac{3}{2})$ |
18.已知条件p:|x+1|>2,条件q:x>a,且¬p是¬q的充分不必要条件,则a的取值范围是( )
| A. | a≤1 | B. | a≤-3 | C. | a≥-1 | D. | a≥1 |
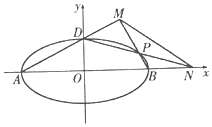 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.