题目内容
设a,b是正数,证明:
≥
•
.
| a3+b3 |
| 2 |
| a2+b2 |
| 2 |
| a+b |
| 2 |
考点:不等式的证明
专题:证明题,不等式的解法及应用
分析:利用分析法证明即可.
解答:
证明:要证明
≥
•
,
只要证明2(a3+b3)≥(a2+b2)(a+b),
只要证明a3+b3≥a2b+ab2,
只要证明(a+b)(a-b)2≥0.当且仅当a=b时等号成立.
∴
≥
•
.
| a3+b3 |
| 2 |
| a2+b2 |
| 2 |
| a+b |
| 2 |
只要证明2(a3+b3)≥(a2+b2)(a+b),
只要证明a3+b3≥a2b+ab2,
只要证明(a+b)(a-b)2≥0.当且仅当a=b时等号成立.
∴
| a3+b3 |
| 2 |
| a2+b2 |
| 2 |
| a+b |
| 2 |
点评:本题考查不等式的证明,考查分析法的运用,正确运用分析法是关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
数列{an}的前n项和记为Sn,a1=1,an+1=2Sn+1(n≥1,n∈N),则数列{an}的通项公式是( )
| A、an=2n |
| B、an=2n-1 |
| C、an=3n-1 |
| D、an=3n |
 如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=a,BC=b,BB1=c,M、N分别是B1C1和AC的中点,求直线MN与底面ABC的夹角的正弦值(或余弦值).
如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=a,BC=b,BB1=c,M、N分别是B1C1和AC的中点,求直线MN与底面ABC的夹角的正弦值(或余弦值).
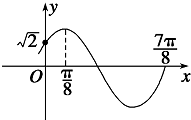 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<