题目内容

7．若4个人报名参加3项体育比赛，每个人限报一项，则不同的报名方法的种数有（　　）
A．A${\;}_{4}^{3}$B．C${\;}_{4}^{3}$C．34D．43

分析 根据题意，分析可得4人中，每人都有3种情况，由分步计数原理计算可得答案．

解答 解：根据题意，4个人报名参加3项体育比赛，每个人限报一项，
则每人都有3项体育比赛可选，即每人都有3种情况，
则不同的报名方法的种数有3×3×3×3=34种；
故选：C．

点评 本题考查分步计数原理的应用，注意没有要求每一项都必须有人报名．

练习册系列答案
相关题目
17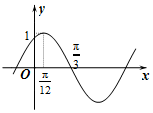．$f（x）=Asin（ωx+φ）（A＞0，|φ|＜\frac{π}{2}）$的图象如图所示，为了得到f（x）的图象，则只要将g（x）=cos2x的图象（　　）
A．向右平移$\frac{π}{12}$个单位长度B．向右平移$\frac{π}{6}$个单位长度
C．向左平移$\frac{π}{12}$个单位长度D．向左平移$\frac{π}{6}$个单位长度
18．如图，已知$\overrightarrow{CA}=\overrightarrow a$，$\overrightarrow{CB}=\overrightarrow b$，AD=2DB，用$\overrightarrow a$、$\overrightarrow b$表示$\overrightarrow{DC}$为（　　）
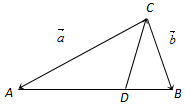
A．$\overrightarrow{DC}=-\frac{5}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$B．$\overrightarrow{DC}$=$-\frac{1}{2}\overrightarrow a-\frac{1}{3}\overrightarrow b$C．$\overrightarrow{DC}$=$-\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$D．$\overrightarrow{DC}=-\frac{1}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$
15．已知f（x）=2xlnx，g（x）=x3+ax2-x+2．
（1）如果函数g（x）的单调递减区间为$（-\frac{1}{3}，1）$，求函数g（x）的解析式；
（2）在（1）的条件下，求函数y=g（x）的图象在点P（-1，g（-1））处的切线方程；
（3）已知不等式f（x）≤g'（x）+2恒成立，若方程aea-m=0恰有两个不等实根，求m的取值范围．
2．与-30°终边相同的角是（　　）
A．-330°B．150°C．30°D．330°
12．数列an=2n+1，其前n项和为Tn，若不等式nlog2（Tn+4）-λ（n+1）+7≥3n对一切n∈N*恒成立，则实数λ的取值范围为（　　）
A．λ≤3B．λ≤4C．2≤λ≤3D．3≤λ≤4
19．已知函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜π）的最小正周期为π，且其图象关于直线$x=\frac{π}{6}$对称．
（1）求ω和φ的值；
（2）若$f（\frac{α}{2}-\frac{π}{12}）=\frac{3}{5}$，α为锐角，求$cos（α-\frac{π}{3}）$的值．
16．函数f（x）=x3-3x-1，若对于区间[-3，2]上的任意x1，x2，都有|f（x1）-f（x2）|≤t，则实数t的最小值是20．
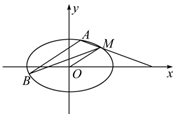17．如图，已知椭圆C的中心在原点，它的一个焦点与抛物线${y^2}=4\sqrt{6}x$的焦点相同，又椭圆C上有一点M（2，1），直线l平行于OM且与椭圆C交于A，B两点，连接MA，MB．
（1）求椭圆C的方程；
（2）求证：直线MA，MB与x轴所构成的三角形总是以x轴上所在线段为底边的等腰三角形．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网