题目内容
14.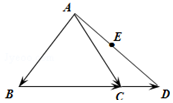 在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )
在△ABC中,已知D是BC延长线上一点,点E为线段AD的中点,若$\overrightarrow{BC}$=2$\overrightarrow{CD}$,且$\overrightarrow{AE}$=λ$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则λ=( )| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
分析 通过利用向量的三角形法则,以及向量共线,代入化简即可得出.
解答 解:∵$\overrightarrow{AE}$=$\frac{1}{2}$$\overrightarrow{AD}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{BD}$)=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$×$\frac{3}{2}$$\overrightarrow{BC}$=)=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{3}{4}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=-$\frac{1}{4}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,
∴λ=-$\frac{1}{4}$,
故选:A.
点评 本题考查了向量共线定理、向量的三角形法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.若0<a<1,0<b<1且a≠b,则在则a+b,$2\sqrt{ab}\;,\;{a^2}+{b^2}$和2ab中最大的是( )
| A. | a+b | B. | 2$\sqrt{ab}$ | C. | a2+b2 | D. | 2ab |
2.与-30°终边相同的角是( )
| A. | -330° | B. | 150° | C. | 30° | D. | 330° |
3.若cos α>0,sin α<0,则角 α的终边在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |