题目内容
10.设函数f(x)=2|x+a|-|x+b|,(Ⅰ)当a=0,b=-$\frac{1}{2}$时,求使f(x)≥$\sqrt{2}$的x取值范围;
(Ⅱ)若f(x)≥$\frac{1}{16}$恒成立,求a-b的取值范围.
分析 (Ⅰ)利用y=2x是增函数,转化f(x)$≥\sqrt{2}$为绝对值不等式,通过$x≥\frac{1}{2}$,$0<x<\frac{1}{2}$,x≤0时,分别求解绝对值不等式.
(Ⅱ)利用f(x)≥$\frac{1}{16}$,转化为绝对值不等式,利用绝对值三角不等式,化简求解即可.
解答 解:(Ⅰ)由于y=2x是增函数,f(x)$≥\sqrt{2}$等价于$|x|-|{x-\frac{1}{2}}|≥\frac{1}{2}$①
当$x≥\frac{1}{2}$时,$|x|-|{x-\frac{1}{2}}|=\frac{1}{2}$,则①式恒成立,
当$0<x<\frac{1}{2}$时,$|x|-|{x-\frac{1}{2}}|=2x-\frac{1}{2}$,①式化为2x≥1,此时①式无解,
当x≤0时,$|x|-|{x-\frac{1}{2}}|=-\frac{1}{2}$,①式无解.
综上,x取值范围是$[{\frac{1}{2},+∞})$…(5分)
(Ⅱ)$f(x)≥\frac{1}{16}?|x+a|-|x+b|≥-4$②
而由||x+a|-|x+b||≤|x+a-x-b|=|a-b|⇒-|a-b|≤|x+a|-|x+b|≤|a-b|
∴要②恒成立,只需-|a-b|≥-4,即|a-b|≤4,
可得a-b的取值范围是[-4,4].…(10分)
点评 本题考查绝对值不等式的解法,考查转化思想以及计算能力.

练习册系列答案
相关题目
20.在平面直角坐标系中,“点M的坐标满足方程4$\sqrt{x}$+y=0”是“点M在曲线y2=16x上”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |


 如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.
如图,在三棱柱ABC-A1B1C1中,G为ABC的重心,延长线段AG交BC于F,B1F交BC1于E.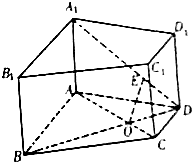 如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.
如图,在四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AB=4,AD=2$\sqrt{2}$,CD=2,AA1=2,侧棱AA1⊥底面ABCD,E是A1D上一点,且A1E=2ED.