题目内容
9.已知函数f(x)=lnx,g(x)=alnx-$\frac{1}{2}$x2,h(x)=$\frac{1}{2}$x2.(1)求函数g(x)的单调区间;
(2)对于函数f(x)与h(x)定义域内的任意实数x,若存在直线y=kx+b,使得f(x)≤kx+b和h(x)≥kx+b都成立,则称直线y=kx+b为函数f(x)与h(x)的分界线,求证:直线y=x-$\frac{1}{2}$为函数f(x)与h(x)的分界线.
分析 (1)通过对g(x)=alnx-$\frac{1}{2}$x2求导可知g′(x)=$\frac{a-{x}^{2}}{x}$,分a≤0与a>0两种情况讨论即可.
(2)通过解析式可知x的取值范围是(0,+∞),通过记m(x)=f(x)-(x-$\frac{1}{2}$)并求导可知m(x)≤m(1),通过记n(x)=h(x)-(x-$\frac{1}{2}$)并求导可知n(x)≥n(1),进而计算可得结论.
解答 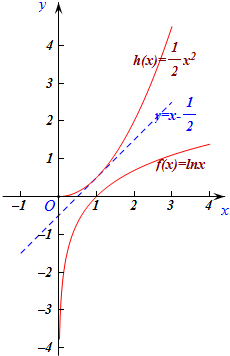 (1)解:∵g(x)=alnx-$\frac{1}{2}$x2,
(1)解:∵g(x)=alnx-$\frac{1}{2}$x2,
∴g′(x)=$\frac{a}{x}$-x=$\frac{a-{x}^{2}}{x}$,
①当a≤0时,显然当x>0时g′(x)恒小于零,
此时函数g(x)在定义域(0,+∞)上单调递减;
②当a>0时,令′(x)=0,解得x=$\sqrt{a}$或x=-$\sqrt{a}$(舍),
∴当0<x<$\sqrt{a}$时函数g(x)单调递增,当x>$\sqrt{a}$时函数g(x)单调递减;
综上所述,当a≤0时函数g(x)的单调递减区间为(0,+∞),
当a>0时函数g(x)的单调递增区间为(0,$\sqrt{a}$)、单调递减区间为($\sqrt{a}$,+∞);
(2)证明:依题意,x的取值范围是(0,+∞),
记m(x)=f(x)-(x-$\frac{1}{2}$)=lnx-x+$\frac{1}{2}$,则m′(x)=$\frac{1}{x}$-1,
∵m(x)的单调递增区间为(0,1)、单调递减区间为(1,+∞),
∴m(x)≤m(1)=0-1+$\frac{1}{2}$=-$\frac{1}{2}$<0,即f(x)≤x-$\frac{1}{2}$;
记n(x)=h(x)-(x-$\frac{1}{2}$)=$\frac{1}{2}$x2-x+$\frac{1}{2}$,则n′(x)=x-1,
∵n(x)的单调递减区间为(0,1)、单调递减增间为(1,+∞),
∴n(x)≥n(1)=$\frac{1}{2}$-1+$\frac{1}{2}$=0,即h(x)≥x-$\frac{1}{2}$;
根据分界线的定义可知,直线y=x-$\frac{1}{2}$为函数f(x)与h(x)的分界线.
点评 本题考查利用导数研究函数的单调性,考查数形结合能力,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.

 口算题天天练系列答案
口算题天天练系列答案| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
| A. | 长度相等的向量叫相等向量 | |
| B. | 零向量的长度为零 | |
| C. | 共线向量是在一条直线上的向量 | |
| D. | 平行向量就是向量所在的直线平行的向量 |
| A. | f(sinx)>f(cosx) | B. | f($\frac{{x}^{2}+1}{2}$)>f(x) | ||
| C. | f($\frac{1}{{3}^{x}+1}$)≥f($\frac{1}{{2}^{x}+1}$) | D. | f($\frac{1}{{3}^{x}+{3}^{-x}}$)≥f($\frac{1}{{2}^{x}+{2}^{-x}}$) |
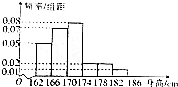 2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.
2016年高考报名体检中,某市共有40000名男生参加体检,体检其中一项为测量身高,统计调查数据显示所有男生的身高服从正态分布N(170,16).统计人员从市一中高三的参加体检的男生中随机抽取了50名进行身高测量,所得数据全部介于162cm和186cm之间,并将测量数据分成6组:第一组[162,166),第二组[166,170),…,第六组[182,186),然后按上述分组方式绘制得到如图所示的频率分布直方图.