题目内容
12.已知命题p:函数f(x)=x3+ax2+x在R上是增函数;命题q:若函数g(x)=ex-x+a在区间[0,+∞)没有零点.(1)如果命题p为真命题,求实数a的取值范围;
(2)命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
分析 (1)如果命题p为真命题,则f′(x)=3x2+2ax+1≥0对x∈(-∞,+∞)恒成立,进而得到实数a的取值范围;
(2)如果命题“p∨q”为真命题,“p∧q”为假命题,则p,q一真一假,进而得到实数a的取值范围.
解答 解:(1)如果命题p为真命题,
∵函数f(x)=x3+ax2+x在R上是增函数,
∴f′(x)=3x2+2ax+1≥0对x∈(-∞,+∞)恒成立…(3分)
∴$△=4{a^2}-12≤0⇒a∈[{-\sqrt{3},\sqrt{3}}]$…(6分)
(2)g′(x)=ex-1≥0对任意的x∈[0,+∞)恒成立,
∴g(x)在区间[0,+∞)递增
命题q为真命题g(0)=a+1>0⇒a>-1…(9分)
由命题“p∨q”为真命题,“p∧q”为假命题知p,q一真一假,
若p真q假,则$\left\{\begin{array}{l}-\sqrt{3}≤a≤\sqrt{3}\\ a≤-1\end{array}\right.⇒a∈[{-\sqrt{3},-1}]$…(11分)
若p假q真,则$\left\{\begin{array}{l}a<-\sqrt{3}或a>\sqrt{3}\\ a>-1\end{array}\right.⇒a∈(\sqrt{3},+∞)$…(13分)
综上所述,$a∈[{-\sqrt{3},-1}]∪(\sqrt{3},+∞)$…(14分)
点评 本题以命题的真假判断与应用为载体,考查了导数法研究函数的单调性,复合命题,函数的零点,难度中档.

练习册系列答案
相关题目
3.若a<b<0,则下列不等式成立的是( )
| A. | ac>bc | B. | $\frac{b}{a}$>1 | C. | |a|>|b| | D. | ($\frac{1}{2}$)a<($\frac{1}{2}$)b |
17.不等式kx2-kx+1>0对一切实数x均成立,则k的取值范围是( )
| A. | 0<k<4 | B. | 0≤k<4 | C. | 0<k≤4 | D. | 0≤k≤4 |
1.在空间直角坐标系中,点A(1,0,1)与点B(2,1,-1)间的距离为( )
| A. | $\sqrt{3}$ | B. | 3 | C. | $\sqrt{6}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
2.设实数x,y满足条件$\left\{\begin{array}{l}{x-y+2≥0}\\{2x-y-4≤0}\\{x≥0,y≥0}\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为 12,则$\frac{3}{a}$+$\frac{4}{b}$的最小值为( )
| A. | $\frac{49}{6}$ | B. | $\frac{25}{6}$ | C. | $\frac{8}{3}$ | D. | 4 |
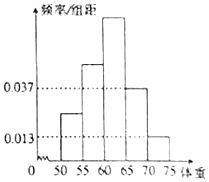 为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.