题目内容
P为正方体ABCD-A1B1C1D1对角线BD1上的一点,且BP=λBD1(λ∈(0,1)).下面命题正确的为: (写出所有正确结论的序号):
①A1D⊥C1P;
②若BD1⊥平面PAC,则λ=
;
③若△PAC为钝角三角形,则λ∈(0,
);
④若λ∈(0,
),则△PAC为锐角三角形.
①A1D⊥C1P;
②若BD1⊥平面PAC,则λ=
| 1 |
| 3 |
③若△PAC为钝角三角形,则λ∈(0,
| 1 |
| 2 |
④若λ∈(0,
| 1 |
| 2 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离,空间角
分析:画出图形,直接判断①A1D⊥C1P的正误;
利用正方体的特征,判断②若BD1⊥平面PAC,则λ=
的正误;
通过λ=
,判断△PAC是否为钝角三角形,判断λ∈(0,
)的正误;
通过建立空间直角坐标系,判断④λ∈(0,
),则△PAC为锐角三角形,判断④的正误.
利用正方体的特征,判断②若BD1⊥平面PAC,则λ=
| 1 |
| 3 |
通过λ=
| 1 |
| 2 |
| 1 |
| 2 |
通过建立空间直角坐标系,判断④λ∈(0,
| 1 |
| 2 |
解答:
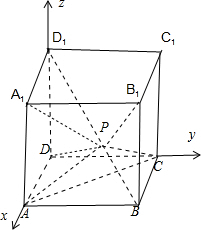 解:如图①中,A1D⊥面ABC1D1,C1P?面ABC1D1 ∴A1D⊥C1P 故①正确;
解:如图①中,A1D⊥面ABC1D1,C1P?面ABC1D1 ∴A1D⊥C1P 故①正确;
对于②若BD1⊥平面PAC,几何体是正方体,∴P在平面AB1C中,则λ=
;②正确;
对于③,当P为BD1的中点时,若△PAC为钝角三角形,设正方体棱长为a,PA=PC=
a,AC=
a,此时∠APC=120°,∴则λ∈(0,
),③不正确;
对于④,建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=1,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1),
∴
=(-1,-1,1),
=λ
=(-λ,-λ,λ),
=
+
=(λ,λ-1,-λ),
=
+
=(λ-1,λ,-λ)
显然∠APC不是平角,所以∠APC为锐角等价于cos∠APC=cos<
,
>=
>0,则等价于
•
>0
即,λ(λ-1)+(λ-1)λ+(-λ)(-λ)=λ(3λ-2)>0,
<λ<1,④不正确;
故答案为:①②.
 解:如图①中,A1D⊥面ABC1D1,C1P?面ABC1D1 ∴A1D⊥C1P 故①正确;
解:如图①中,A1D⊥面ABC1D1,C1P?面ABC1D1 ∴A1D⊥C1P 故①正确;对于②若BD1⊥平面PAC,几何体是正方体,∴P在平面AB1C中,则λ=
| 1 |
| 3 |
对于③,当P为BD1的中点时,若△PAC为钝角三角形,设正方体棱长为a,PA=PC=
| ||
| 2 |
| 2 |
| 1 |
| 2 |
对于④,建立如图所示的空间直角坐标系,不妨设正方体的棱长|AB|=1,则A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,0),A1(1,0,1),B1(1,1,1),C1(0,1,1),D1(0,0,1),
∴
| BD1 |
| BP |
| BD1 |
| PA |
| PB |
| BA |
| PC |
| PB |
| BC |
显然∠APC不是平角,所以∠APC为锐角等价于cos∠APC=cos<
| PA |
| PC |
| ||||
︳
|
| PA |
| PC |
即,λ(λ-1)+(λ-1)λ+(-λ)(-λ)=λ(3λ-2)>0,
| 2 |
| 3 |
故答案为:①②.
点评:本题考查空间直角坐标系的应用,夹角与距离的关系,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
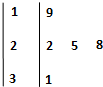 已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )
已知某篮球运动员2013年度参加了25场比赛,若从中抽取5场,用茎叶图统计该运动员5场中的得分如图所示,则该样本的方差为 ( )| A、4 | ||
B、
| ||
| C、18 | ||
| D、16 |