题目内容
已知数列{an},a1=2,an+1=
an,(n∈N*).
(1)求a2,a3,a4,猜测通项公式;
(2)用数学归纳法证明你的结论.
| n+2 |
| n |
(1)求a2,a3,a4,猜测通项公式;
(2)用数学归纳法证明你的结论.
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:(1)利用已知条件通过n=1,2,3即可求a2,a3,a4;
(2)由(1)a1,a2,a3,a4;猜想数列{an}的通项公式,利用用数学归纳法的证明步骤在证明即可.
(2)由(1)a1,a2,a3,a4;猜想数列{an}的通项公式,利用用数学归纳法的证明步骤在证明即可.
解答:
解:(1)由a1=2,an+1=
an,(n∈N*).
所以a2=
×2=6,…(2分)
同理a3=
×6=12,a4=
×12=20…(4分)
(2)猜想an=n(n+1)…(6分)
证明:①当n=1时,猜想成立.…(7分)
②设当n=k时(n∈N*)时,猜想成立,即ak=k(k+1),…(8分)
则当n=k+1时,有ak+1=
•ak=
•k(k+1)=(k+1)(k+2),…(12分)
所以当n=k+1时猜想也成立
综合①②,猜想对任何n∈N*都成立 …(14分)
| n+2 |
| n |
所以a2=
| 1+2 |
| 1 |
同理a3=
| 2+2 |
| 2 |
| 3+2 |
| 3 |
(2)猜想an=n(n+1)…(6分)
证明:①当n=1时,猜想成立.…(7分)
②设当n=k时(n∈N*)时,猜想成立,即ak=k(k+1),…(8分)
则当n=k+1时,有ak+1=
| k+2 |
| k |
| k+2 |
| k |
所以当n=k+1时猜想也成立
综合①②,猜想对任何n∈N*都成立 …(14分)
点评:本题考查归纳推理,数学归纳法的证明步骤的应用,考查计算能力与逻辑推理能力.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
若
(2x-3)dx=4,则正数t=( )
| ∫ | t 0 |
| A、1 | B、2 | C、3 | D、4 |
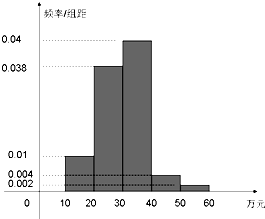 在某市的人大贿选案中,经调查统计该市人大代表的受贿情况的频率分布直方图如图:其中受贿[10,20]万元的有10人.
在某市的人大贿选案中,经调查统计该市人大代表的受贿情况的频率分布直方图如图:其中受贿[10,20]万元的有10人. 如图,已知P是圆O外一点,PA为 圆O的切线.A为切点.割线PBC经过圆心O,若PA=3
如图,已知P是圆O外一点,PA为 圆O的切线.A为切点.割线PBC经过圆心O,若PA=3