题目内容
已知椭圆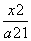 +
+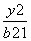 =1(a1>b1>0)与双曲线
=1(a1>b1>0)与双曲线 -
-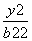 =1(a2>0,b2>0)有公共焦点F1、F2,设P是它们的一个交点.
=1(a2>0,b2>0)有公共焦点F1、F2,设P是它们的一个交点.
(1)试用b1,b2表示△F1PF2的面积;
(2)当b1+b2=m(m>0)是常数时,求△F1PF2的面积的最大值.
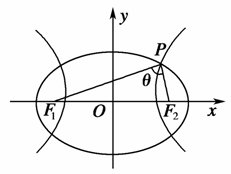
[解析] (1)如图所示,
令∠F1PF2=θ.
因|F1F2|=2c,则a -b
-b =a
=a +b
+b =c2.即a
=c2.即a -a
-a =b
=b +b
+b .
.
由椭圆、双曲线定义,得
|PF1|+|PF2|=2a1,|PF1|-|PF2|=2a2(令|PF1|>|PF2|),
所以|PF1|=a1+a2,|PF2|=a1-a2,
 所以sinθ=
所以sinθ= .所以S△F1PF2=
.所以S△F1PF2= |PF1|·|PF2|sinθ
|PF1|·|PF2|sinθ
= (a
(a -a
-a )·
)· =b1b2.
=b1b2.
(2)当b1+b2=m(m>0)为常数时
S△F1PF2=b1b2≤ =
= ,
,
所以△F1PF2面积的最大值为 .
.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
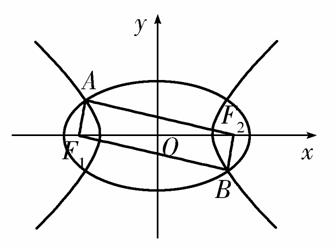
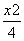 +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )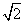 B.
B.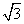
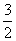 D.
D.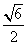
 x3-f ′(-1)·x2+x+5,则f ′(1)=________.
x3-f ′(-1)·x2+x+5,则f ′(1)=________.