题目内容
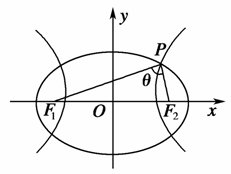
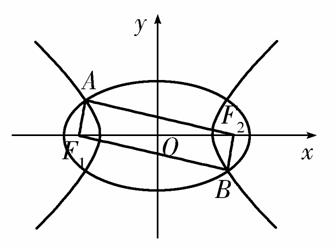
如图,F1、F2是椭圆C1: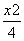 +y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A、B分别是C1、C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
A.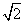 B.
B.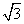
C.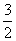 D.
D.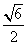
D
[解析] 不妨设双曲线方程为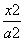 -
-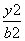 =1.
=1.
由题意知|BF1|-|BF2|=2a⇒|BF1|2+|BF2|2-2|BF1|·|BF2|=4a2,①
并由勾股定理得|BF1|2+|BF2|2=4c2=12,②
由①②知12-4a2=2|BF1|·|BF2|,
∴|BF1|·|BF2|=6-2a2.下面求|BF1|·|BF2|的值.
在椭圆中|BF1|+|BF2|=4,故|BF1|2+|BF2|2+2|BF1|·|BF2|=16,
又由②知|BF1|2+|BF2|2=4c2=12,
∴|BF1|·|BF2|=2,因此有c2-a2=1,
∵c2=3,∴a2=2,∴C2的离心率e=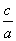 =
=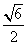 .
.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
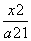 +
+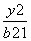 =1(a1>b1>0)与双曲线
=1(a1>b1>0)与双曲线 -
-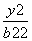 =1(a2>0,b2>0)有公共焦点F1、F2,设P是它们的一个交点.
=1(a2>0,b2>0)有公共焦点F1、F2,设P是它们的一个交点.