题目内容
点P是双曲线C1:
-
=1(a>0,b>0)与圆C2:x2+y2=a2+b2的一个交点,且2∠PF1F2=∠PF2F1,其中F1,F2分别为双曲线C1的左右焦点,则双曲线C1的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意,求出∠PF1F2=
,得出|PF2|、|PF1|的大小,再利用双曲线的定义,求出c与a的关系,即得离心率的值.
| π |
| 6 |
解答:
解:如图所示,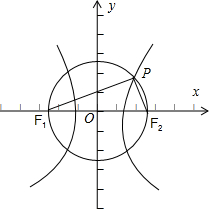
∵F1F2圆C2:x2+y2=a2+b2的直径,∴∠F1PF2是直角;
∴在Rt△PF1F2中,2∠PF1F2=∠PF2F1,
∴∠PF1F2=
,
∴|PF2|=
|F1F2|=c,
∴|PF1|=
|PF2|=
c,
∴|PF1|-|PF2|=
c-c=2a,
∴
=
=
+1.
故答案为:
+1.

∵F1F2圆C2:x2+y2=a2+b2的直径,∴∠F1PF2是直角;
∴在Rt△PF1F2中,2∠PF1F2=∠PF2F1,
∴∠PF1F2=
| π |
| 6 |
∴|PF2|=
| 1 |
| 2 |
∴|PF1|=
| 3 |
| 3 |
∴|PF1|-|PF2|=
| 3 |
∴
| c |
| a |
| 2 | ||
|
| 3 |
故答案为:
| 3 |
点评:本题考查了双曲线的定义与几何性质的应用问题,解题时应根据题意画出图形,结合图形解答问题,是基础题.

练习册系列答案
相关题目
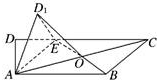 如图,在梯形ABCD中,AB∥CD,∠ADC=90°,AB=2,DC=3,AD=1.E是DC上一点,且DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=30°,设AC与BE的交点为O.
如图,在梯形ABCD中,AB∥CD,∠ADC=90°,AB=2,DC=3,AD=1.E是DC上一点,且DE=1,连接AE,将△DAE沿AE折起到△D1AE的位置,使得∠D1AB=30°,设AC与BE的交点为O.