题目内容
求函数y=(
)x+(
)x+1的值域.
| 1 |
| 4 |
| 1 |
| 2 |
考点:指数型复合函数的性质及应用
专题:函数的性质及应用
分析:函数y=(
)x+(
)x+1=[(
)x]2+(
)x+1对其进行配方,判断出它的值域即可.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:y=(
)x+(
)x+1
=[(
)x]2+(
)x+1
=[(
)x+
]2+
,
∵(
)x+
>
,
∴[(
)x+
]2>
,
∴[(
)x+
]2+
>1,
∴函数y=(
)x+(
)x+1的值域为(1,+∞).
| 1 |
| 4 |
| 1 |
| 2 |
=[(
| 1 |
| 2 |
| 1 |
| 2 |
=[(
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∵(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴[(
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
∴函数y=(
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查指数函数的值域,解题的关键是对所给的解析式进行配方,根据指数函数的值域与二次函数的性质判断出函数的值域

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱PA=PC=2
四棱锥P-ABCD的底面是边长为2的菱形,∠DAB=60°,侧棱PA=PC=2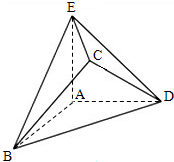 如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2
如图,在几何体ABCDE中,AB=AD=BC=DC=2,AE=2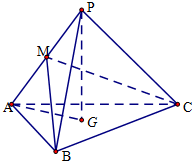 如图,三棱锥P-ABC中,AB=AC=2
如图,三棱锥P-ABC中,AB=AC=2 如图,圆O的直径AB=5,C是圆上一点,过点A的圆O切线交BC的延长线于点D,且AD=
如图,圆O的直径AB=5,C是圆上一点,过点A的圆O切线交BC的延长线于点D,且AD=