题目内容
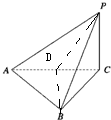
 如图所示,在四面体P-ABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B-AP-C的余弦值为( )
如图所示,在四面体P-ABC中,PC⊥平面ABC,AB=BC=CA=PC,那么二面角B-AP-C的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:二面角的平面角及求法
专题:空间位置关系与距离
分析:设AB=BC=CA=PC=a.知平面PAC⊥平面ABC,取AC的中点D连接BD,PD,得△PAD为△PAB在平面PAC的投影.二面角B-AP-C为α,由投影定理得cosα=
.
| S△PAD |
| S△PAB |
解答:
解:设AB=BC=CA=PC=a.
知平面PAC⊥平面ABC,取AC的中点D连接BD,PD,
知BD⊥AC,故D为B点在平面PAC的投影.而△PAD为△PAB在平面PAC的投影.
△PAD的面积为:S=
×1×1×
a2=
,
△PAB中,PA=PB=
a,AB=a.
由余弦定理,解得cos∠APB=
=
.
从而sin∠APB=
.
△PAB的面积为S′=
×
×
×
×
=
,
设二面角B-AP-C为α,
由投影定理得cosα=
=
=
.
故答案为:
.
知平面PAC⊥平面ABC,取AC的中点D连接BD,PD,
知BD⊥AC,故D为B点在平面PAC的投影.而△PAD为△PAB在平面PAC的投影.
△PAD的面积为:S=
| 1 |
| 2 |
| 1 |
| 2 |
| a2 |
| 4 |

△PAB中,PA=PB=
| 2 |
由余弦定理,解得cos∠APB=
| 2+2-1 |
| 2×2 |
| 3 |
| 4 |
从而sin∠APB=
| ||
| 4 |
△PAB的面积为S′=
| a2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| ||
| 4 |
| ||
| 4 |
设二面角B-AP-C为α,
由投影定理得cosα=
| S |
| S′ |
| ||||
|
| ||
| 7 |
故答案为:
| ||
| 7 |
点评:本题考查二面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知i是虚数单位,则化简复数
的结果为( )
| -1+i |
| 1+i |
| A、i | B、-1 | C、-i | D、1 |
边长为5,7,8的三角形的最大角与最小角的和是( )
| A、90° | B、150° |
| C、135° | D、120° |
将函数f(x)=sin(ωx+
)的图象关于x=
对称,则ω的值可能是( )
| π |
| 6 |
| π |
| 6 |
A、
| ||
B、
| ||
| C、5 | ||
| D、2 |
下列说法中不正确的是( )
| A、点斜式y-y1=k(x-x1)适用于不垂直于x轴的任何直线 | ||||
| B、斜截式y=kx+b适用于不垂直于x轴的任何直线 | ||||
C、两点式
| ||||
D、截距式
|
某几何体的三视图如图所示,则该几何体的表面积为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知圆O:x2+y2=4,从这个圆上任意一点P向y轴作垂线段PP1(P1在y轴上),M在直线PP1上且
=2
,则动点M的轨迹方程是( )
| P1M |
| P1P |
| A、4x2+16y2=1 | ||||
| B、16x2+4y2=1 | ||||
C、
| ||||
D、
|