Question

11．已知函数f（x）=$\left\{\begin{array}{l}{4|lo{g}_{2}x|，0＜x＜2}\\{\frac{1}{2}{x}^{2}-5x+12，x≥2}\end{array}\right.$，若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（　　）

• A． （16，21）
• B． （16，24）
• C． （17，21）
• D． （18，24）

Answer 1

分析 根据图象可判断：$\frac{1}{2}$＜a＜1，1＜b＜2，2＜c＜4，6＜d＜8，当直线y=t，0＜t＜4，可以有4个交点，通过图象运动可以判断1×1×4×6=24，$\frac{1}{2}×2×2×8$=16，直线越往上走abcd的积越小，越往下abcd的积越大，即可求出答案．

解答 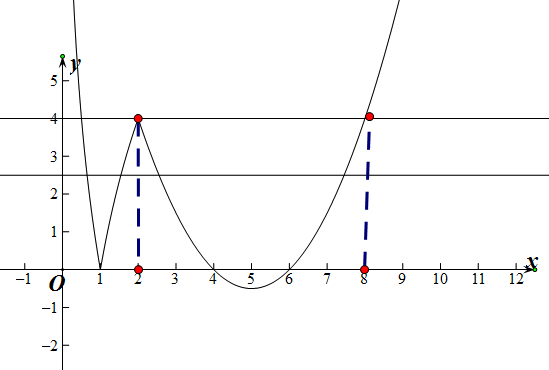 解：若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0
根据图象可判断：$\frac{1}{2}$＜a＜1，1＜b＜2，2＜c＜4，6＜d＜8，
当直线y=t，0＜t＜4，可以有4个交点，把直线向上平移，向下平移，可判断：直线越往上走abcd的积越小，越往下abcd的积越大，
当t=0时1×1×4×6=24，当t=4时，$\frac{1}{2}×2×2×8$=16，abcd的取值范围是（16，24），
故选：B．

点评 本题综合考查了函数图象的运用，求解两个图象的交点问题，运用动的观点解决，理解好题意是解题关键．