题目内容
1.已知f(x)=2|x|,则∫${\;}_{-2}^{4}$f(x)dx=$\frac{18}{ln2}$.分析 由∫${\;}_{-2}^{4}$f(x)dx=${∫}_{-2}^{0}$($\frac{1}{2}$)xdx+${∫}_{0}^{4}$2xdx,再根据定积分的法则计算即可.
解答 解:f(x)=2|x|=$\left\{\begin{array}{l}{{2}^{x},x≥0}\\{(\frac{1}{2})^{x},x<0}\end{array}\right.$,
∴∫${\;}_{-2}^{4}$f(x)dx=${∫}_{-2}^{0}$($\frac{1}{2}$)xdx+${∫}_{0}^{4}$2xdx=$\frac{\frac{1}{{2}^{x}}}{ln\frac{1}{2}}$|${\;}_{-2}^{0}$+$\frac{{2}^{x}}{ln2}$|${\;}_{0}^{4}$=$\frac{3}{ln2}$+$\frac{15}{ln2}$=$\frac{18}{ln2}$,
故答案为:$\frac{18}{ln2}$.
点评 本题考查了定积分的法则和分部积分法,属于基础题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
11.已知函数f(x)=$\left\{\begin{array}{l}{4|lo{g}_{2}x|,0<x<2}\\{\frac{1}{2}{x}^{2}-5x+12,x≥2}\end{array}\right.$,若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0,则abcd的取值范围是( )
| A. | (16,21) | B. | (16,24) | C. | (17,21) | D. | (18,24) |
10. 如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
 如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )
如图,已知F1,F2是椭圆C:$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左右焦点,点P在椭圆C上,线段PF2与圆x2+y2=b2相切于点Q,若点Q为线段PF2的中点,则b的值为( )| A. | $\sqrt{3}$ | B. | 2 | C. | $\sqrt{6}$ | D. | 2$\sqrt{2}$ |
11.函数f(x)=$\frac{1}{3}$x3+x在点处(1,$\frac{4}{3}$)的切线与坐标轴围成的三角形的面积为( )
| A. | 3 | B. | $\frac{1}{3}$ | C. | 2 | D. | $\frac{1}{9}$ |
 上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.
上海迪士尼乐园有一块长方形地ABCD,若要在此地块上拟建一个Rt△MNP的主题乐园,已知AB=2km,AD=$\sqrt{3}$km,点M是AB的中点,点P在线段AD上,点N在线段BC上,记∠NMB=α.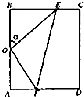 某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
某休闲农庄有一块长方形鱼塘ABCD,AB=100米,BC=50$\sqrt{3}$米,为了便于游客休闲散步,该农庄决定在鱼塘内建3条如图所示的观光走廊OE、EF和OF,考虑到整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上(不含顶点),且∠EOF=90°.($\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)