题目内容
已知函数f(x)的定义域为R,若f(x+1)与f(x-1)都是奇函数,则f(x+3)是 .
考点:抽象函数及其应用
专题:函数的性质及应用
分析:首先由奇函数性质求f(x)的周期,然后利用此周期推导出结果
解答:
解:∵f(x+1)与f(x-1)都是奇函数,
∴函数f(x)关于点(1,0)及点(-1,0)对称,
∴f(x)+f(2-x)=0,f(x)+f(-2-x)=0,
故有f(2-x)=f(-2-x),
函数f(x)是周期T=[2-(-2)]=4的周期函数.
∴f(-x-1+4)=-f(x-1+4),
f(-x+3)=-f(x+3),
f(x+3)是奇函数.
故答案为:奇函数
∴函数f(x)关于点(1,0)及点(-1,0)对称,
∴f(x)+f(2-x)=0,f(x)+f(-2-x)=0,
故有f(2-x)=f(-2-x),
函数f(x)是周期T=[2-(-2)]=4的周期函数.
∴f(-x-1+4)=-f(x-1+4),
f(-x+3)=-f(x+3),
f(x+3)是奇函数.
故答案为:奇函数
点评:本题主要考查奇函数性质的灵活运用,并考查函数周期的求法.

练习册系列答案
相关题目
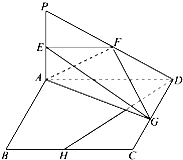 如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且AD=2PA,E,F,G,H分别是线段PA,PD,CD,BC的中点.
如图所示,PA⊥平面ABCD,四边形ABCD为正方形,且AD=2PA,E,F,G,H分别是线段PA,PD,CD,BC的中点. 函数f(x)=ax2+bx+c的图象如图所示,求b的取值范围.
函数f(x)=ax2+bx+c的图象如图所示,求b的取值范围.