题目内容
17.已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和圆:${x^2}+{y^2}={(\frac{b}{2}+c)^2}({c^2}={a^2}-{b^2})$有四个不同的公共点,则椭圆的离心率的取值范围是( )| A. | $(\frac{{\sqrt{5}}}{5},\frac{3}{5})$ | B. | $(\frac{{\sqrt{2}}}{5},\frac{{\sqrt{5}}}{5})$ | C. | $(\frac{{\sqrt{2}}}{5},\frac{3}{5})$ | D. | $(0,\frac{{\sqrt{5}}}{5})$ |
分析 由椭圆与圆有四个不同的交点,则满足b<$\frac{b}{2}+c$<a,由椭圆的简单几何性质,求得$\frac{1}{5}$a2<c2<$\frac{9}{25}$a2,根据椭圆的离心率即可求得椭圆的离心率的取值范围.
解答 解:由椭圆和圆的几何性质可知,椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$
和圆:${x^2}+{y^2}={(\frac{b}{2}+c)^2}({c^2}={a^2}-{b^2})$有四个不同的公共点,
满足b<$\frac{b}{2}+c$<a,解得:$\frac{{b}^{2}}{4}<$c2=a2-b2<(a-$\frac{b}{2}$)2,
则有$\frac{4}{5}$a<b<$\frac{2\sqrt{5}}{5}$a,$\frac{16}{25}$a2<b2<$\frac{4}{5}$a2,则$\frac{16}{25}$a2<a2-c2<$\frac{4}{5}$a2,
∴$\frac{1}{5}$a2<c2<$\frac{9}{25}$a2,
由椭圆的离心率e=$\frac{c}{a}$,
∴$\frac{\sqrt{5}}{5}$<e<$\frac{3}{5}$,
故选A.
点评 本题考查椭圆的标准方程及简单几何性质,考查不等式的解法,考查计算能力,属于中档题.

练习册系列答案
相关题目
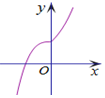
8.已知函数f(x)=$\left\{\begin{array}{l}{ax+b,x≤0}\\{lo{g}_{c}(x+\frac{1}{9}),x>0}\end{array}\right.$的图象如图所示,则a+b+c=( )
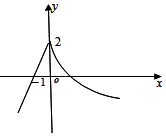

| A. | $\frac{10}{3}$ | B. | $\frac{13}{3}$ | C. | 3 | D. | $\frac{9}{10}$ |
20.已知x>-1,则$x+\frac{4}{x+1}$的最小值为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |