题目内容
12.对于命题:①“若 x2+y2=0,则 x,y全为0”的逆命题;
②“全等三角形是相似三角形”的否命题;
③“若 m>0,则x2+x-m=0有实根”的逆否命题.
其中真命题的题号是①③.
分析 ①,逆命题为:若 x,y全为0,则 x2+y2=0;
②,不全等三角形也可以相似;
③,原命题为真,其逆否命题与原命题同真假.
解答 解:对于①,“若 x2+y2=0,则 x,y全为0”的逆命题为:若 x,y全为0,则 x2+y2=0为真命题;
对于②,“全等三角形是相似三角形”的否命题为:“不全等三角形不是相似三角形”,因为不全等三角形也可以相似,故为假命题;
对于③,“当 m>0时,方程x2+x-m=0的△=1+4m>0,方程有实根”,原命题为真,其逆否命题与原命题同真假,故为真命题.
故答案为:①③
点评 本题考查了命题的四种形式及其真假的判定,属于基础题.

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
20.三棱锥SABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )
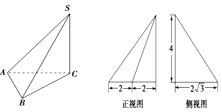

| A. | 4$\sqrt{2}$ | B. | $\sqrt{19}$ | C. | $\sqrt{20}$ | D. | $4\sqrt{3}$ |
7.在物理实验中,为了研究所挂物体的重量x对弹簧长度y的影响.某学生通过实验测量得到物体的重量与弹簧长度的对比表:
(1)利用最小二乘法求y对x的回归直线方程;
(2)预测所挂物体重量为8g时的弹簧长度.
(参考公式及数据:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}},a=\overline y-b\overline x$,$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$)
| 物体重量(单位g) | 1 | 2 | 3 | 4 | 5 |
| 弹簧长度(单位cm) | 1.5 | 3 | 4 | 5 | 6.5 |
(2)预测所挂物体重量为8g时的弹簧长度.
(参考公式及数据:$b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x•\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{\overline x}^2}}},a=\overline y-b\overline x$,$\sum_{i=1}^5{{x_i}^2}=55$$\sum_{i=1}^5{{x_i}{y_i}}=72$)
17.已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和圆:${x^2}+{y^2}={(\frac{b}{2}+c)^2}({c^2}={a^2}-{b^2})$有四个不同的公共点,则椭圆的离心率的取值范围是( )
| A. | $(\frac{{\sqrt{5}}}{5},\frac{3}{5})$ | B. | $(\frac{{\sqrt{2}}}{5},\frac{{\sqrt{5}}}{5})$ | C. | $(\frac{{\sqrt{2}}}{5},\frac{3}{5})$ | D. | $(0,\frac{{\sqrt{5}}}{5})$ |
4.在棱锥P-ABC中,侧棱PA、PB、PC两两垂直,Q为底面△ABC内一点,若点Q到三个侧面的距离分别为3、4、5,则以线段PQ为直径的球的体积为( )
| A. | $\frac{125π}{6}$ | B. | $\frac{{125\sqrt{2}π}}{3}$ | C. | $\frac{50π}{3}$ | D. | $\frac{25π}{3}$ |
1.已知F1,F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{16}$=1(a>0)的左右焦点,点A在双曲线的右支上,点P(7,2)是平面内一定点,若对任意实数m,直线4x+3y+m=0与双曲线C至多有一个公共点,则|AP|+|AF2|的最小值为( )
| A. | 2$\sqrt{37}$-6 | B. | 10-3$\sqrt{5}$ | C. | 8-$\sqrt{37}$ | D. | 2$\sqrt{5}$-2 |