题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{ax+b,x≤0}\\{lo{g}_{c}(x+\frac{1}{9}),x>0}\end{array}\right.$的图象如图所示,则a+b+c=( )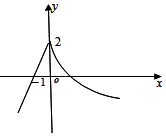
| A. | $\frac{10}{3}$ | B. | $\frac{13}{3}$ | C. | 3 | D. | $\frac{9}{10}$ |
分析 先由图象可求得直线的方程,又函数的图象过点(0,2),将其坐标代入可得c值,从而即可求得a+b+c的值.
解答 解:由图象可求得直线的方程为y=2x+2,
又函数y=logc(x+$\frac{1}{9}$)的图象过点(0,2),
将其坐标代入可得c=$\frac{1}{3}$,
所以a+b+c=2+2+$\frac{1}{3}$=$\frac{13}{3}$.
故选:B
点评 本题考查了函数图象的识别和应用,属于基础题.

练习册系列答案
相关题目
18.为了了解某校学生喜欢吃辣是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人抽到喜欢吃辣的学生的概率为$\frac{3}{5}$.
(1)请将上面的列表补充完整;
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由:
下面的临界值表供参考:
(参考公式:${K^2}=\frac{{n•{{({ad-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$,其中n=a+b+c+d)
| 喜欢吃辣 | 不喜欢吃辣 | 合计 | |
| 男生 | 40 | 10 | 50 |
| 女生 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(2)是否有99.9%以上的把握认为喜欢吃辣与性别有关?说明理由:
下面的临界值表供参考:
| p(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
19.下列命题中为真命题的是( )
| A. | 命题“若$\overrightarrow{a}$∥$\overrightarrow{c}$且$\overrightarrow{b}$∥$\overrightarrow{c}$,则$\overrightarrow{a}$∥$\overrightarrow{b}$” | |
| B. | 命题“若x>2015,则x>0”的逆命题 | |
| C. | 命题“若xy=0,则x=0或y=0”的否命题 | |
| D. | 命题“若x2≥1,则x≥1”的逆否命题 |
16.设集合M={-1,0,1},N={-2,-1,0,2},则M∩N=( )
| A. | {0} | B. | {1,0} | C. | (-1,0) | D. | {-1,0} |
13.三个数a=0.32,b=0.32.1,c=20.3的大小关系是( )
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | b<c<a |
20.三棱锥SABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为( )
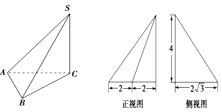

| A. | 4$\sqrt{2}$ | B. | $\sqrt{19}$ | C. | $\sqrt{20}$ | D. | $4\sqrt{3}$ |
17.已知椭圆:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和圆:${x^2}+{y^2}={(\frac{b}{2}+c)^2}({c^2}={a^2}-{b^2})$有四个不同的公共点,则椭圆的离心率的取值范围是( )
| A. | $(\frac{{\sqrt{5}}}{5},\frac{3}{5})$ | B. | $(\frac{{\sqrt{2}}}{5},\frac{{\sqrt{5}}}{5})$ | C. | $(\frac{{\sqrt{2}}}{5},\frac{3}{5})$ | D. | $(0,\frac{{\sqrt{5}}}{5})$ |