题目内容
2.化简:(1)$\frac{si{n}^{2}35°-\frac{1}{2}}{cos10°cos80°}$
(2)($\frac{1}{tan\frac{α}{2}}$-tan$\frac{α}{2}$)•$\frac{1-cos2α}{sin2α}$.
分析 (1)利用降幂公式,诱导公式,二倍角的正弦函数公式化简所求即可化简求值得解;
(2)利用同角三角函数基本关系式,二倍角公式化简即可得解.
解答 解:(1)$\frac{si{n}^{2}35°-\frac{1}{2}}{cos10°cos80°}$=$\frac{\frac{1-cos70°}{2}-\frac{1}{2}}{cos10°sin10°}$=$\frac{-\frac{1}{2}cos70°}{\frac{1}{2}sin20°}$=-1.
(2)($\frac{1}{tan\frac{α}{2}}$-tan$\frac{α}{2}$)•$\frac{1-cos2α}{sin2α}$=($\frac{cos\frac{α}{2}}{sin\frac{α}{2}}$-$\frac{sin\frac{α}{2}}{cos\frac{α}{2}}$)•$\frac{2si{n}^{2}α}{2sinαcosα}$=$\frac{cosα}{\frac{1}{2}sinα}$•$\frac{sinα}{cosα}$=2.
点评 本题主要考查了降幂公式,诱导公式,二倍角公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
17.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出5名学生,将这50名学生随机编号1~50号,并分组,第一组1~10号,第二组11~20号,…,第五组41~50号,若在第三组中抽得号码为22的学生,则在第五组中抽得号码为( )的学生.
| A. | 42 | B. | 44 | C. | 46 | D. | 48 |
11.若直线l的一个方向向量$\overrightarrow a=(2,2,-2)$,平面α的一个法向量为$\overrightarrow b=(1,1,-1)$,则( )
| A. | l∥α | B. | l⊥α | C. | l?α | D. | A、C都有可能 |
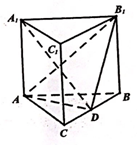 如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.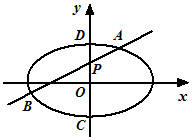 如图,椭圆E:$\frac{x^2}{4}+\frac{y^2}{b^2}=1(0<b<2)$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}•\overrightarrow{PD}=-2$
如图,椭圆E:$\frac{x^2}{4}+\frac{y^2}{b^2}=1(0<b<2)$,点P(0,1)在短轴CD上,且$\overrightarrow{PC}•\overrightarrow{PD}=-2$