题目内容
17.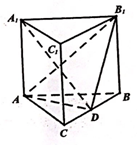 如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.
如图,已知在直三棱柱ABC-A1B1C1中,AB=AA1=2,二面角A-C1C-B的大小为$\frac{π}{3}$,点D线段BC的中点.(1)若AB=AC,求证:平面BB1C1C⊥平面AB1D;
(2)当三棱柱ABC-A1B1C1的体积最大时,求直线A1D与平面AB1D所成角θ的正弦值.
分析 (1)若AB=AC,证明:AD⊥平面BB1C1C,即可证明平面BB1C1C⊥平面AB1D;
(2)当三棱柱ABC-A1B1C1的底面积最大时,体积最大,利用等体积方法求出A1到平面AB1D的距离,即可求直线A1D与平面AB1D所成角θ的正弦值.
解答 (1)证明:由题意,∠ACB=$\frac{π}{3}$,AB=AC,
∴△ABC为正三角形,∴AD⊥BC,AD⊥CC1,
∴AD⊥平面BB1C1C,
∵AD?平面AB1D,
∴平面BB1C1C⊥平面AB1D;
(2)解:当三棱柱ABC-A1B1C1的底面积最大时,体积最大,
∵4=AB2=$A{C}^{2}+B{C}^{2}-2AC•BC•\frac{1}{2}$≥AC•BC-AC•BC=AC•BC,
∴当AC=BC,三角形ABC为正三角形时面积取最大值,
设A1到平面AB1D的距离为d,则由等体积可得$\frac{1}{3}{S}_{△A{B}_{1}D}•d=\frac{1}{3}•\frac{1}{2}•AD•D{B}_{1}•d=\frac{\sqrt{3}}{3}$,
∴d=$\frac{2}{\sqrt{5}}$,
∴sinθ=$\frac{d}{{A}_{1}D}=\frac{\frac{2}{\sqrt{5}}}{\sqrt{7}}$=$\frac{2\sqrt{35}}{35}$.
点评 本题考查线面、面面垂直的证明,考查线面角,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
8.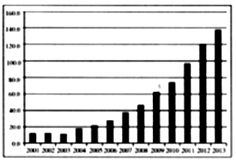 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
 2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )
2001年至2013年北京市电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述这13年间电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=aax+b | D. | y=alnx+b |
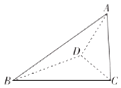 已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.
已知三棱锥A-BCD的四个顶点A、B、C、D都在球O的表面上,AC⊥平面BCD,BC⊥CD,且AC=$\sqrt{3}$,BC=2,CD=$\sqrt{5}$,则球O的表面积为12π.


