题目内容

已知P1（x1，y1），P2（x2，y2）是以原点O为圆心的单位圆上的两点，∠P1OP2=θ（θ为钝角）．若sin（θ+
π
4
）=
3
5
，则x1x2+y1y2的值为
 
．
考点：两角和与差的正弦函数,任意角的三角函数的定义
专题：三角函数的求值,平面向量及应用
分析：根据题意表示出
OP1
•
OP2
，根据向量数量积的运算求得x1x2+y1y2=cosθ，进而根据sin（θ+
π
4
）的值，求得cosθ的值．
解答： 解：依题意知
OP1
=（x₁，y₁）
OP2
=（x₂，y₂）
OP1
•
OP2
=x1x2+y1y2，
另外P₁，P₂在单位圆上，|
OP1
|=|
OP2
|=1
OP1
•
OP2
=|
OP1
|•|
OP2
|cosθ=1•1•cosθ=cosθ，
∴x1x2+y1y2=cosθ，
∵sin（θ+
π
4
）=
2
2
sinθ+
2
2
cosθ=
3
5
，①
sin2θ+cos2θ=1，②，且θ为钝角
联立①②求得 cosθ=-
2
10
．
故答案为：-
2
10
．
点评：本题主要考查了是平面向量的运算，平面向量数量积的应用．注重了对学生基础知识的考查．
练习册系列答案
相关题目
已知函数f（x）=x-（a+1）lnx-
a
x
（a∈R），g（x）=
x
ex
．
（Ⅰ）求f（x）的单调区间；
（Ⅱ）当a＜1时，若存在x1∈[1，2]，使得对任意的x2∈[1，2]，f（x1）＜g（x2）恒成立，求a的取值范围．
平行四边形ABCD中，AB=2，AD=2
2
，∠BAD=45°，以BD为折线，把△ABD折起，使平面ABD⊥平面CBD，连结AC．

（Ⅰ）求证：AB⊥DC；
（Ⅱ）求二面角B-AC-D的大小．
设函数f（x）=-
a
2
x2+（a+1）x-lnx（a∈R）．
（1）当a=0时，求函数f（x）的极值；
（2）当a＞0时，讨论函数f（x）的单调性；
（3）若对任意a∈（2，3）及任意x1，x2∈[1，2]，恒有
a2-1
2
m+ln2＞|f（x1）-f（x2）|成立，求实数m的取值范围．
在△ABC中，∠A，∠B，∠C的对边分别为a，b，c，若bcosC=（2a-c）cosB，
（Ⅰ）求∠B的大小；
（Ⅱ）若b=
7
，a-c=2，求△ABC的面积．
利用函数的单调性比较大小：
（1）sin508°与sin144°；         
（2）cos760°与cos（-770°）
（3）tan（-
π
5
）与tan（-
3π
7
）．
设函数f（x）=cos（
3
x+φ）（0＜φ＜π），若f（x）+f′（x）是偶函数，则φ=
 
．
一个农技站为了考察某种麦穗长的分布情况，在一块试验地里抽取了100个麦穗，量得长度如下（单位：cm）：
6.5　6.4　6.7　5.8　5.9　5.9　5.2　4.0　5.4　4.6
5.8　5.5　6.0　6.5　5.1　6.5　5.3　5.9　5.5　5.8
6.2　5.4　5.0　5.0　6.8　6.0　5.0　5.7　6.0　5.5
6.8　6.0　6.3　5.5　5.0　6.3　5.2　6.0　7.0　6.4
6.4　5.8　5.9　5.7　6.8　6.6　6.0　6.4　5.7　7.4
6.0　5.4　6.5　6.0　6.8　5.8　6.3　6.0　6.3　5.6
5.3　6.4　5.7　6.7　6.2　5.6　6.0　6.7　6.7　6.0
5.6　6.2　6.1　5.3　6.2　6.8　6.6　4.7　5.7　5.7
5.8　5.3　7.0　6.0　6.0　5.9　5.4　6.0　5.2　6.0
6.3　5.7　6.8　6.1　4.5　5.6　6.3　6.0　5.8　6.3
根据上面的数据列出频率分布表、绘出频率分布直方图，并估计长度在5.75～6.05cm之间的麦穗在这批麦穗中所占的百分比．
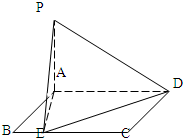如图，四边形ABCD为矩形，且AD=4，AB=2，PA=1，PA⊥平面ABCD，E为线段BC上的动点．
（1）当E为线段BC的中点时，求证：DE⊥平面PAE；
（2）若BE=1，求二面角P-ED-A的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网