题目内容
平行四边形ABCD中,AB=2,AD=2
,∠BAD=45°,以BD为折线,把△ABD折起,使平面ABD⊥平面CBD,连结AC.
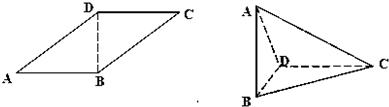
(Ⅰ)求证:AB⊥DC;
(Ⅱ)求二面角B-AC-D的大小.
| 2 |

(Ⅰ)求证:AB⊥DC;
(Ⅱ)求二面角B-AC-D的大小.
考点:二面角的平面角及求法,直线与平面垂直的性质
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)在△ABD中,利用余弦定理,可得BD,从而可得AB⊥BD,根据平面ABD⊥平面CBD,可得AB⊥平面CBD,从而可得AB⊥DC;
(Ⅱ)建立空间直角坐标系,求出平面ABC的法向量
=(1,1,0),平面DAC的法向量
=(1,0,-1),利用向量的夹角公式,可得二面角B-AC-D平面角的大小.
(Ⅱ)建立空间直角坐标系,求出平面ABC的法向量
| n |
| m |
解答:
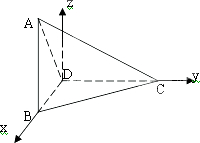 (Ⅰ)证明:在△ABD中,∵AB=2,AD=2
(Ⅰ)证明:在△ABD中,∵AB=2,AD=2
,
BD2=AB2+AD2-2AB×AD×cos45°=4,∴BD=2,
∴AD2=AB2+BD2,∴AB⊥BD,
∵平面ABD⊥平面CBD,平面ABD∩平面CBD=BD
∴AB⊥平面CBD,
∵DC?平面CBD,
∴AB⊥DC;
(Ⅱ)解:在四面体ABCD中,以D为原点,DB为x轴,DC为y轴,过D垂直于平面BDC的射线为z轴,建立如图空间直角坐标系,则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)
设平面ABC的法向量为
=(x,y,z),则
∵
=(0,0,2),
=(-2,2,0),
∴
,∴取
=(1,1,0).
同理可得平面DAC的法向量为
=(1,0,-1).
∴cos<
,
>=
∴二面角B-AC-D平面角的大小为60°.
 (Ⅰ)证明:在△ABD中,∵AB=2,AD=2
(Ⅰ)证明:在△ABD中,∵AB=2,AD=2| 2 |
BD2=AB2+AD2-2AB×AD×cos45°=4,∴BD=2,
∴AD2=AB2+BD2,∴AB⊥BD,
∵平面ABD⊥平面CBD,平面ABD∩平面CBD=BD
∴AB⊥平面CBD,
∵DC?平面CBD,
∴AB⊥DC;
(Ⅱ)解:在四面体ABCD中,以D为原点,DB为x轴,DC为y轴,过D垂直于平面BDC的射线为z轴,建立如图空间直角坐标系,则D(0,0,0),B(2,0,0),C(0,2,0),A(2,0,2)
设平面ABC的法向量为
| n |
∵
| BA |
| BC |
∴
|
| n |
同理可得平面DAC的法向量为
| m |
∴cos<
| m |
| n |
| 1 |
| 2 |
∴二面角B-AC-D平面角的大小为60°.
点评:本题考查面面垂直,考查线面垂直,考查面面角,考查利用向量的方法解决面面角问题,确定平面的法向量是关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
某校在一天的6节课中随机安排语文、数学、英语三门文化课和音乐、体育、美术三种艺术课各一节,则在课表上的相邻2节文化课之间至少间接一节艺术课的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|