题目内容
已知函数f(x)=x-(a+1)lnx-
(a∈R),g(x)=
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当a<1时,若存在x1∈[1,2],使得对任意的x2∈[1,2],f(x1)<g(x2)恒成立,求a的取值范围.
| a |
| x |
| x |
| ex |
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当a<1时,若存在x1∈[1,2],使得对任意的x2∈[1,2],f(x1)<g(x2)恒成立,求a的取值范围.
考点:利用导数研究函数的单调性,导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,即可求f(x)的单调区间;
(Ⅱ)将不等式f(x1)<g(x2)恒成立,转化为求出函数的最值关系,即可求a的取值范围.
(Ⅱ)将不等式f(x1)<g(x2)恒成立,转化为求出函数的最值关系,即可求a的取值范围.
解答:
解:(Ⅰ)函数f(x)的都为(0,+∞),
则f′(x)=1-
+
=
=
,
①若a≤0,由f′(x)>0,得x>1.此时函数单调递增,即增区间为(1,+∞),
由f′(x)<0,得0<x<1.此时函数单调递减,即减区间为(0,1),
②若0<a<1,由f′(x)>0,得x>1或0<x<a.此时函数单调递增,即增区间为(1,+∞),(0,a),
由f′(x)<0,得a<x<1.此时函数单调递减,即减区间为(a,1),
③若a=1时,f′(x)≥0,此时函数单调递增,即增区间为(0,+∞);
④若a>1,由f′(x)>0,得x>a或0<x<1.此时函数单调递增,即增区间为(a,+∞),(0,1),
由f′(x)<0,得1<x<a.此时函数单调递减,即减区间为(1,a).
(Ⅱ)当a<1时,若存在x1∈[1,2],使得对任意的x2∈[1,2],f(x1)<g(x2)恒成立,
则f(x)min<g(x)min
由Ⅰ知,f(x)在[1,2]上为增函数,则f(x)min=f(1)=1-a,
∵g(x)=
.
∴g′(x)=
≤0,即g(x)在[1,2]上为减函数,
则g(x)min=g(2)=
,
故1-a<
,即1-
<a<1.
则f′(x)=1-
| a+1 |
| x |
| a |
| x2 |
| x2-(a+1)x+a |
| x2 |
| (x-a)(x-1) |
| x2 |
①若a≤0,由f′(x)>0,得x>1.此时函数单调递增,即增区间为(1,+∞),
由f′(x)<0,得0<x<1.此时函数单调递减,即减区间为(0,1),
②若0<a<1,由f′(x)>0,得x>1或0<x<a.此时函数单调递增,即增区间为(1,+∞),(0,a),
由f′(x)<0,得a<x<1.此时函数单调递减,即减区间为(a,1),
③若a=1时,f′(x)≥0,此时函数单调递增,即增区间为(0,+∞);
④若a>1,由f′(x)>0,得x>a或0<x<1.此时函数单调递增,即增区间为(a,+∞),(0,1),
由f′(x)<0,得1<x<a.此时函数单调递减,即减区间为(1,a).
(Ⅱ)当a<1时,若存在x1∈[1,2],使得对任意的x2∈[1,2],f(x1)<g(x2)恒成立,
则f(x)min<g(x)min
由Ⅰ知,f(x)在[1,2]上为增函数,则f(x)min=f(1)=1-a,
∵g(x)=
| x |
| ex |
∴g′(x)=
| 1-x |
| ex |
则g(x)min=g(2)=
| 2 |
| e2 |
故1-a<
| 2 |
| e2 |
| 2 |
| e2 |
点评:本题主要考查函数单调性的判断,求出函数的导数,根据导数和函数单调性之间的关系是解决本题的关键.
注意要对a进行分类讨论.
注意要对a进行分类讨论.

练习册系列答案
相关题目
如图的框图的功能是计算表达式1+2+3+…+10的值,则在①、②两处应填入( )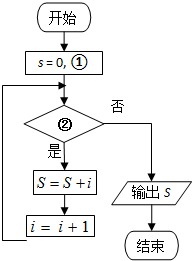

| A、i=0,i≤10 |
| B、i=0,i<10 |
| C、i=1,i≤10 |
| D、i=1,i<10 |
某校在一天的6节课中随机安排语文、数学、英语三门文化课和音乐、体育、美术三种艺术课各一节,则在课表上的相邻2节文化课之间至少间接一节艺术课的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知一组数据为0,-1,4,12,6,6,则这组数据的众数与中位数之和是( )
| A、10 | B、11 | C、13 | D、14 |