题目内容
14.若定义在R上的函数f(x),g(x)满足f(x-1)=f(1-x),g(x)=f(x-2),且f(x1)>f(x2)>f(1)(x1>x2>0),g(0)=3,g(2)=1,若g(x)在[0,m]上有最小值1,最大值3,则m的取值范围是( )| A. | (0,+∞) | B. | (0,2] | C. | [2,4] | D. | [2,+∞) |
分析 由题意可得f(x)在定义域R上是偶函数且在[0,+∞)上是增函数,从而可得g(x)的图象关于x=2对称,且在[2,+∞)上是增函数,从而解得.
解答 解:∵f(x-1)=f(1-x),
∴f(x)在定义域R上是偶函数,
又∵对x1>x2>0,f(x1)>f(x2)>f(0);
∴f(x)在[0,+∞)上是增函数,
故g(x)的图象关于x=2对称,且在[2,+∞)上是增函数,
而g(0)=f(-2)=3,g(2)=f(0)=1,
故g(4)=g(0)=3,
∵g(x)在[0,m]上有最小值1,最大值3,
∴m∈[2,4],
故选:C.
点评 本题考查了函数的性质的判断及数形结合的思想应用.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
19.点A(1,1)在直线l:mx+ny=1上,则mn的最大值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | 1 |
6.等比数列{an}中,a1+a2=4,a2+a3=12,则a3与a4的等差中项为( )
| A. | 6 | B. | 12 | C. | 9 | D. | 18 |
3.“x=2”是“(x-2)•(x+5)=0”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
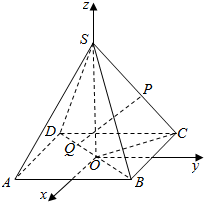 在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.
在正四棱锥S-ABCD中,底面边长为a,侧棱长也为a,以底面中心O为坐标原点,建立如图所示的空间直角坐标系,P点在侧棱SC上,Q点在底面ABCD的对角线BD上,试求P、Q两点间的最小距离.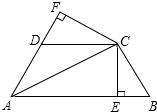 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD. 满足
满足 ,则
,则 ____________.
____________.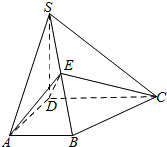 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,SD=2,E为棱SB上的一点,且SE=2EB,CE与平面SAB所成角的正弦值为$\frac{\sqrt{30}}{10}$.