题目内容
3.计算下列式子的值:(1)$\frac{2lg2+lg3}{1+\frac{1}{2}lg0.36+\frac{1}{3}lg8}$;
(2)$sin\frac{25π}{6}+cos\frac{25π}{3}+tan(-\frac{25π}{4})$.
分析 (1)由条件利用对数的运算性质,计算求得结果.
(2)由条件利用诱导公式,计算求得结果.
解答 解:(1)原式=$\frac{lg4+lg3}{1+lg0.6+lg2}$=$\frac{lg12}{1+lg1.2}$=$\frac{lg12}{lg10+lg1.2}$=1.
(2)原式=$sin\frac{π}{6}+cos\frac{π}{3}+tan(-\frac{π}{4})$=$\frac{1}{2}+\frac{1}{2}{-}1=0$.
点评 本题主要考查对数的运算性质,诱导公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.已知点P是边长为2的正方形内任一点,则点P到四个顶点的距离均大于1的概率是( )
| A. | $\frac{π}{4}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{π}{3}$ |
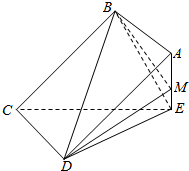 如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD
如图,矩形ABCD所在平面与三角形ECD所在平面相交于CD,AE⊥平面ECD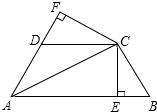 如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.
如图,已知AC平分∠BAD,CE⊥AB于点E,CF⊥AD于点F,且BC=CD.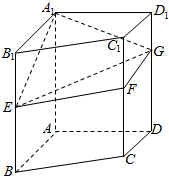 如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.
如图直四棱柱ABCD-A1B1C1D1,底面ABCD是直角梯形,AB∥DC,∠BAD=90°,AA1=AB=2CD=4,AD=2,E、F、G分别是侧棱BB1、C1C、DD1上的点,BE=2,DG=3.