题目内容
3.△ABC中,AB=3,AC=2BC,当△ABC面积取最大值时,C角的正弦值为$\frac{3}{5}$.分析 由题意设AC=2BC=2x,由三边关系可得1<x<3,由余弦定理和同角三角函数基本关系可得可得sinC,进而可得S的表达式,由二次函数的最值可得.
解答 解:由题意设BC=x,则AC=2BC=2x,
由三角形三边关系可得$\left\{\begin{array}{l}{x+2x>3}\\{3+x>2x}\end{array}\right.$,解得1<x<3,
由余弦定理可得cosC=$\frac{{x}^{2}+4{x}^{2}-9}{2•x•2x}$=$\frac{5{x}^{2}-9}{4{x}^{2}}$,
∴sinC=$\sqrt{1-co{s}^{2}C}$=$\frac{3\sqrt{-({x}^{4}-10{x}^{2}+9)}}{4{x}^{2}}$,
∴△ABC面积S=$\frac{1}{2}$•x•2x•$\frac{3\sqrt{-({x}^{4}-10{x}^{2}+9)}}{4{x}^{2}}$=$\frac{3}{4}$$\sqrt{-({x}^{4}-10{x}^{2}+9)}$,
当x2=-$\frac{-10}{2×1}$即x=$\sqrt{5}$时,上式取最大值3,
此时sinC=$\frac{3\sqrt{-({x}^{4}-10{x}^{2}+9)}}{4{x}^{2}}$=$\frac{3}{5}$,
故答案为:$\frac{3}{5}$.
点评 本题考查解三角形,涉及正余弦定理和三角形的面积公式以及二次函数的最值,属中档题.

练习册系列答案
相关题目
11.给出下列命题,①在空间中,若$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ∈R),则$\overrightarrow{a}$∥$\overrightarrow{b}$:②在空间中,$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$=λ$\overrightarrow{b}$(λ∈R),下列说法正确的是( )
| A. | ①是真命题,②是假命题 | B. | ①是假命题,②是真命题 | ||
| C. | ①②都是真命题 | D. | ①②都是假命题 |
2.已知a=1.7-2.5,b=2.51.7,c=${log_2}{\frac{2}{3}}$,则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
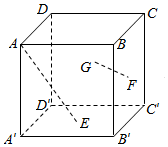 在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?
在正方体ABCD-A′B′C′D′中,E,F,G分别是面A′C′,面B′C,面CD′的中心,则AE与FG所成的角大小为多少?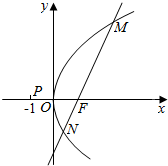 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.