题目内容

已知函数f（x）=
log3x，x＞0
3x，x≤0
，若f（x）=
1
3
，则x的值为（　　）
A、
1
27
或-1
B、
33
或-1
C、
1
3
或-1
D、-1
考点：对数的运算性质
专题：函数的性质及应用
分析：对x分类讨论，利用指数函数与对数函数的单调性即可得出．
解答： 解：当x＞0时，由log3x=
1
3
，解得x=
33
．
当x≤0时，由3x=
1
3
，解得x=-1．
综上可得：x=
33
或-1．
故选：B．
点评：本题考查了分类讨论思想方法、指数函数与对数函数的单调性，属于基础题．
练习册系列答案
相关题目
已知命题p：方程
x2
9-2k
+
y2
k
=1表示焦点在x轴上的椭圆；命题q：方程
x2
2
-
y2
k
=1表示双曲线，且离心率e∈（
2
，
3
），若命题p∧q为假命题，p∨q为真命题，求实数k的取值范围．
数列{an}为等差数列，若a2+a8=
2
3
π，则tan（a3+a7）的值为（　　）
A、
3
3
B、-
3
3
C、
3
D、-
3
已知函数f（x）=4sin
ω x
2
cos （
ω x
2
+
π
3
）+
3
（x∈R，ω＞0）的最小正周期为4π．
（Ⅰ） 求函数f（x）的最大值；
（Ⅱ） 若α∈（0，
π
2
），且f（α-
π
2
）=
6
5
，求f（α）的值．
已知a，b，c分别为锐角△ABC三个内角A，B，C的对边，2bsinC=
3
c
（Ⅰ）求角B的大小；
（Ⅱ）若b=2，△ABC的面积为
3
，求a，c的值．
函数f（x）=log0.5（x2-1）的单调递增区间是
 
．
已知角α的终边与单位圆x2+y2=1交于P(
1
2
，y0)，则cos2α等于
 
．
函数f（x）=lg（1-x）的定义域为（　　）
A、[0，1]
B、（-1，+∞）
C、[-1，1]
D、（-∞，1）
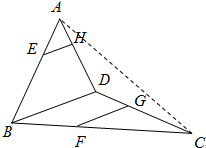如图，空间四边形ABCD中，E、H为AB、AD的中点，G、F为BC、CD上的点，且
CF
CB
=
CG
CD
．
（Ⅰ）证明：EH∥BD；
（Ⅱ）若FE∩GH=M，判断点M是否在直线AC上，并证明你的结论．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网