题目内容
8.已知函数f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$),x∈R.(I)求函效f(x)的最小正周期和单调递增区间;
(2)当x∈[-$\frac{π}{8}$,$\frac{π}{2}$]时,方程f(x)=k恰有两个不同的实数根.求实数k的取值范围;
(3)将函数f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$)的图象向右平移m(m>0)个单位后所得函数g(x)的图象关于原点中心对称,求m的最小值.
分析 (I)由条件利用余弦函数的周期性、单调性得出结论.
(2)根据余弦函数的图象,数形结合可得k的范围.
(3)由条件利用y=Asin(ωx+φ)的图象变换规律,三角函数的奇偶性,求得m的最小正值.
解答 解:(I)对于函数f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$),它的最小正周期为$\frac{2π}{2}$=π,
令2kπ-π≤2x-$\frac{π}{4}$≤2kπ,求得kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,可得函数的增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
(2)当x∈[-$\frac{π}{8}$,$\frac{π}{2}$]时,2x-$\frac{π}{4}$∈[-$\frac{π}{2}$,$\frac{3π}{4}$],结合f(x)的图象,
可得方程f(x)=k恰有两个不同的实数根时,
f(x)的图象和直线y=k有2个交点,数形结合求得求实数0≤k<$\sqrt{2}$.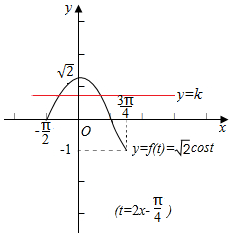
(3)将函数f(x)=$\sqrt{2}$cos(2x-$\frac{π}{4}$)的图象向右平移m(m>0)个单位后,
所得函数g(x)=$\sqrt{2}$cos(2x-2m-$\frac{π}{4}$)的图象关于原点中心对称,
∴2m+$\frac{π}{4}$=kπ+$\frac{π}{2}$,即 m=$\frac{kπ}{2}$+$\frac{π}{8}$,k∈Z,
故m的最小值为$\frac{π}{8}$.
点评 本题主要考查余弦函数的周期性、单调性,余弦函数的图象特征,y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
3.已知数列{an}满足a1=3,an=-an-1-2n+1,在a26,a27,a29,a29,a30中,最大的一项是( )
| A. | a26 | B. | a27 | C. | a28 | D. | a29 | ||||
| E. | a30 |
17.空间9个点分布异面直线L1、L2上,L1上有4个点,L2上有5个点,则由它们可确定异面直线的对数为( )
| A. | 121对 | B. | 108对 | C. | 21对 | D. | 60对 |
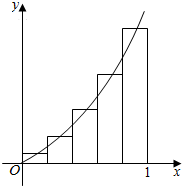 求由抛物线f(x)=x2,直线x=1以及x轴所围成的平面图形的面积时,若将区间[0,1]5等分,如图所示,以小区间中点的纵坐标为高,所有小矩形的面积之和为0.33.
求由抛物线f(x)=x2,直线x=1以及x轴所围成的平面图形的面积时,若将区间[0,1]5等分,如图所示,以小区间中点的纵坐标为高,所有小矩形的面积之和为0.33.