题目内容
9.设集合A={x|$\frac{1}{32}$≤2x≤4},B={x|m-1<x<2m+1},若A∪B=A,求m的取值范围.分析 先化简集合A,再分类讨论即可求出m的取值范围.
解答 解:集合A={x|$\frac{1}{32}$≤2x≤4}={x|-5≤x≤2},B={x|m-1<x<2m+1},
∵A∪B=A,
∴B⊆A,
①当B=∅时,满足B⊆A,此时m-1≥2m+1,即m≤-2;
②当B≠∅,即m>-2时,
∴$\left\{\begin{array}{l}{m-1<2m+1}\\{m-1≥-5}\\{2m+1≤2}\end{array}\right.$,
解得-2<m≤$\frac{1}{2}$,
综上所述m的取值范围是:(-∞,$\frac{1}{2}$].
点评 本题考查了集合的包含关系判断及应用,考查了不等式的解法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.目标函数z=x-y,在如图所示的可行域内(阴影部分且包括边界),使z取得最小值的点的坐标为( )


| A. | (1,1) | B. | (3,2) | C. | (5,2) | D. | (4,1) |
4.已知$\overrightarrow{a}$=(sinωx,1),$\overrightarrow{b}$=(1,cosωx),f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$的周期为π,则f(x)的一个对称中心为( )
| A. | ($\frac{π}{4}$,0) | B. | (-$\frac{π}{4}$,0) | C. | ($\frac{π}{8}$,0) | D. | (-$\frac{π}{8}$,0) |
1.下列函数中,与y=x-1为同一函数的是( )
| A. | y=$\sqrt{{{(x-1)}^2}}$ | B. | y=$\root{3}{{{{(x-1)}^3}}}$ | C. | y=$\frac{{{x^2}-1}}{x+1}$ | D. | $y={(\sqrt{x-1})^2}$ |
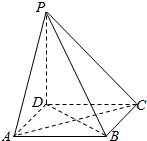 如图,四棱锥P-ABCD的各棱长都为a.
如图,四棱锥P-ABCD的各棱长都为a.