题目内容
已知椭圆x2+2y2=12,A是x轴正方向上的一定点,若过点A,斜率为1的直线被椭圆截得的弦长为
,点A的坐标是________.
答案：(2,0)
解析：设A(x0,0)(x0＞0),则直线l的方程为y=x-x0,设直线l与椭圆相交于P(x1,y1)、Q(x2,y2)，由y=x-x0可得3x2-4x0x+2x02-12=0,
x1+x2=,x1·x2=
,则
|x1-x2|=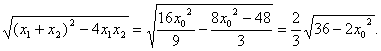
∴
∴x02=4.又x0＞0,∴x0=2.∴A(2,0).
练习册系列答案
相关题目
已知椭圆x2+2y2=4，则以（1，1）为中点的弦的长度是（ ）
A、3
| ||||
B、2
| ||||
C、
| ||||
D、
|
已知椭圆x2+2y2-4=0，则以M（1，1）为中点的弦所在的直线方程是（ ）
| A、x+2y-3=0 | B、2x+y-3=0 | C、x-2y+3=0 | D、2x-y+3=0 |