题目内容
已知函数f(x)＝－2sin2x＋2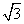
sinxcosx＋1.
(1) 求f(x)的最小正周期及对称中心；
(2) 若x∈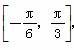
，求f(x)的最大值和最小值．
[审题视点] 逆用二倍角公式，化为正弦型函数再求解．
解：(1) f(x)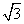＝sin2x＋cos2x＝2sin
，所以f(x)的最小正周期为T＝
＝π.令sin＝0，则x＝
(k∈Z)，所以f(x)的对称中心为
(k∈Z)．
(2) 因为x∈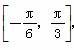，所以－
≤2x＋≤
.所以－
≤sin≤1，所以－1≤f(x)≤2.所以当x＝－时，f(x)的最小值为－1；当x＝时，f(x)的最大值为2.
练习册系列答案
相关题目
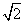，b＝2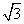
，cosC＝
，则△ABC的面积为________．
sinAsinx的值域．
，α∈
，则sin2α＝__________．
，tanα＝
的值．
，且
，则cos2θ＝________．
，α是第二象限角，且tan(α＋β)＝1，则tan2β＝________．