题目内容
4.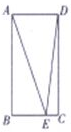 在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )
在如图所示的矩形ABCD中,AB=4,AD=2,E为线段BC上的点,则$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为( )| A. | 12 | B. | 15 | C. | 17 | D. | 16 |
分析 以B为坐标原点,分别以BC、BA所在直线为x、y轴建立平面直角坐标系,得到A、D的坐标,设出E的坐标,利用数量积的坐标运算求解.
解答 解:建立如图所示平面直角坐标系,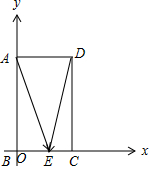
则A(0,4),D(2,4),
设E(x,0)(0≤x≤2),
则$\overrightarrow{AE}=(x,-4)$,$\overrightarrow{DE}=(x-2,-4)$.
∴$\overrightarrow{AE}•\overrightarrow{DE}=x(x-2)+16$=x2-2x+16=(x-1)2+15.
∴当x=1时,$\overrightarrow{AE}•\overrightarrow{DE}$的最小值为15.
故选:B.
点评 本题考查平面向量的数量积运算,建系起到事半功倍的效果,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知函数f(x)=3sinx-4cosx(x∈R)的一个对称中心是(x0,0),则tanx0的值为( )
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
12.已知ω为正整数,若函数f(x)=sinωx+cosωx在区间(-$\frac{π}{3}$,$\frac{π}{6}$)内单调递增,则函数f(x)最小正周期为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | π | D. | 2π |
3.在极坐标系中,点$(2,\frac{π}{3})$与点(1,0)的距离为( )
| A. | 2 | B. | $\sqrt{4+\frac{π^2}{9}}$ | C. | $\sqrt{1+\frac{π^2}{9}}$ | D. | $\sqrt{3}$ |
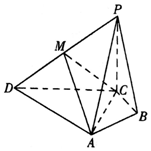 在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.
在四棱锥P-ABCD中,PC⊥底面ABCD,M是PD的中点,AC⊥AD,BA⊥BC,PC=AC=2BC,∠ACD=∠ACB.