题目内容
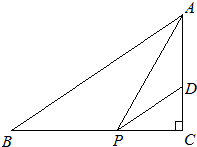 如图,直角△ABC中,∠C=90°,AB=2
如图,直角△ABC中,∠C=90°,AB=2| 5 |
| ||
| 5 |
(1)求AC、BC的长;
(2)设PC的长为x,△ADP的面积为y.当x为何值时,y最大,并求出最大值.
考点:函数最值的应用
专题:综合题,函数的性质及应用
分析:(1)在Rt△ABC中,根据角的正弦的定义建立等式求出AC,再由勾股定理求BC;
(2)根据题设建立起面积的函数,再由函数的性质求出最大值即可.
(2)根据题设建立起面积的函数,再由函数的性质求出最大值即可.
解答:
解:(1)在Rt△ABC中,sinB=
,AB=2
,得
=
,∴AC=2,根据勾股定理得:BC=4.
(2)∵PD∥AB,∴△ABC∽△DPC,∴
=
=
设PC=x,则DC=
x,AD=2-
x
∴S△ADP=
AD•PC=
(2-
x)•x=-
x2+x=-
(x-2)2+1
∴当x=2时,y的最大值是1.
| ||
| 5 |
| 5 |
| AC |
| AB |
| ||
| 5 |
(2)∵PD∥AB,∴△ABC∽△DPC,∴
| DC |
| PC |
| AC |
| BC |
| 1 |
| 2 |
设PC=x,则DC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ADP=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴当x=2时,y的最大值是1.
点评:本题考查了函数的应用及解直角三角形,最值问题一般的思路是建立其函数关系,由函数的性质求解.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
已知数列{xn}满足xn+3=xn,xn+2=|xn+1-xn|(n∈N*),若x1=1,x2=a(a≤1且a≠0),则数列{xn}的前2016项的和等于( )
| A、671 | B、760 |
| C、1324 | D、1344 |
下列命题错误的是( )
| A、在△ABC中,“A>B”是“sinA>sinB”的充要条件 | ||||||||||||
B、点(
| ||||||||||||
C、若|
| ||||||||||||
| D、“sinα=sinβ”的充要条件是“α+β=(2k+1)π或α-β=2kπ(k∈Z)” |
一个数列{an}的首项a1=1,an=2an-1+1(n≥2),则数列{an}的第4项是( )
| A、7 | B、15 | C、31 | D、12 |
设等比数列{an}的前n项和为{an},若S3=3,S6=15,则S9=( )
| A、31 | B、32 | C、63 | D、64 |