题目内容
9.设f(x)是R上的偶函数,且在(-∞,0)上是增函数,并满足f(2a2+a+1)<f(2a2-2a+3),则实数a的取值范围是a>$\frac{2}{3}$.分析 根据二次函数的性质结合函数单调性和奇偶性之间的关系,解不等式即可得到结论.
解答 解:2a2+a+1=2(a+$\frac{1}{4}$)2+$\frac{7}{8}$>0,2a2-2a+3=2(a-$\frac{1}{2}$)2+$\frac{5}{2}$>0
∵偶函数f(x)在(-∞,0)上是增函数,
∴f(x)在(0,+∞)上是减函数,
若f(2a2+a+1)<f(2a2-2a+3),
则2a2+a+1>2a2-2a+3,即3a-2>0,
解得a>$\frac{2}{3}$,
故答案为:a>$\frac{2}{3}$.
点评 本题主要考查不等式的求解,利用函数奇偶性和单调性的关系是解决本题的关键.

练习册系列答案
相关题目
19.如图,已知一个八面体的各条棱长均为1,四边形ABCD 为正方形,则下列命题中的假命题是( )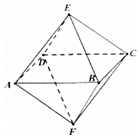

| A. | 不平行的两条棱所在的直线所成的角是60o或90o | |
| B. | 四边形AECF是正方形 | |
| C. | 点A到平面BCE的距离为$\frac{\sqrt{6}}{3}$ | |
| D. | 该八面体的顶点不会在同一个球面上. |
20.设Sn是等差数列{an}的前n项和,且S5<S6=S7>S8,则下列结论错误的是( )
| A. | d<0 | B. | a7=0 | ||
| C. | S${\;}_{{9}_{\;}}$>S5 | D. | S6和S7均为Sn的最大值 |
4.《张丘建算经》中女子织布问题为:某女子善于织布,一天比一天织得快,且从第2天开始,每天比前一天多织相同量的布,已知第一天织5尺布,一月(按30天计)共织390尺布,则从第2天起每天比前一天多织( )尺布.
| A. | $\frac{1}{2}$ | B. | $\frac{8}{15}$ | C. | $\frac{16}{31}$ | D. | $\frac{16}{29}$ |
14.已知a.b.c.d成等比数列,且曲线y=x2-2x+3的顶点是(b,c),则a+d等于( )
| A. | 3 | B. | 2 | C. | $\frac{9}{2}$ | D. | -2 |
18.能够保证直线a∥平面β的条件是( )
| A. | b?β,a∥b | B. | a∥b∥c,b?β,c?β | ||
| C. | a?β,b?β,a∥b | D. | b?β,A、B∈a,C、D∈b,AC=BD |